Over one billion dollars have been spent in the US to split up big schools into smaller ones because small schools regularly show up in rankings as top performers.
In this post, I will show you why that money was wasted because of a widespread (but not so well known) statistical artifact, so read on!
Continue reading “The Most Dangerous Equation, or Why Small is Not Beautiful!”
One of the most fiercely fought debates in quantitative finance is whether the stock market (or financial markets in general) is (are) efficient, i.e. whether you can find patterns in them that can be profitably used.
If you want to learn about an ingenious method (that is already present in anyone’s computer) to approach that question, read on!
Continue reading “Is the Stock Market Efficient? Let your ZIP Compression Tool give an Answer!”
What is the “opposite” of sampling without replacement? In a classical urn model sampling without replacement means that you don’t replace the ball that you have drawn. Therefore the probability of drawing that colour becomes smaller. How about the opposite, i.e. that the probability becomes bigger? Then you have a so-called Pólya urn model!
Many real-world processes have this self-reinforcing property, e.g. leading to the distribution of wealth or the number of followers on social media. If you want to learn how to simulate such a process with R and encounter some surprising results, read on!
Continue reading “The Pólya Urn Model: A simple Simulation of “The Rich get Richer””
The Bundesliga is Germany’s primary football league. It is one of the most important football leagues in the world, broadcast on television in over 200 countries.
If you want to get your hands on a tool to forecast the result of any game (and perform some more statistical analyses), read on!
Continue reading “New Bundesliga Forecasting Tool: Can Underdog Hertha Berlin beat Bayern Munich?”
In view of the current dramatic events in Afghanistan many wonder why the extensive international efforts to bring some stability to the country have failed so miserably.
In this post, we will present and analytically examine a fascinating theory that seems to be able to explain political (in-)stability almost mono-causally, so read on!
Continue reading “The “Youth Bulge” of Afghanistan: The Hidden Force behind Political Instability”
Over the course of the last two and a half years, I have written over one hundred posts for my blog “Learning Machines” on the topics of data science, i.e. statistics, artificial intelligence, machine learning, and deep learning.
I use many of those in my university classes and in this post, I will give you the first part of a learning path for the knowledge that has accumulated on this blog over the years to become a well-rounded data scientist, so read on!
Continue reading “Learning Path for “Data Science with R” – Part I”
Everybody is talking about big data but the real skill lies in the art of inferring useful information from only a handful of values!
If you want to learn how to determine the range of the typical value of a dataset (i.e. the median) with just five values and why this works, read on!
Continue reading “The Small Data Rule: Infer the Big Picture from only Five Values!”
In this post, we will first give some intuition for and then demonstrate what is often called the most beautiful formula in mathematics, Euler’s identity, in R – first numerically with base R and then also symbolically, so read on!
Continue reading “Euler Coding Challenge: Build Maths’ Most Beautiful Formula in R”
One of the big sensations of the UEFA Euro 2020 is that Switzerland kicked out world champion France. We take this as an opportunity to share with you a simple statistical model to predict football (soccer) results with R, so read on!
Continue reading “Euro 2020: Will Switzerland kick out Spain too?”
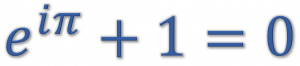
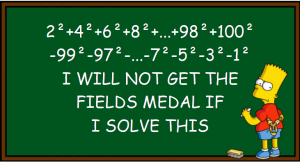This time we want to solve the following simple task with R: Take the numbers 1 to 100, square them, and add all the even numbers while subtracting the odd ones!
If you want to see how to do that in at least seven different ways in R, read on!
Continue reading “R Coding Challenge: 7 (+1) Ways to Solve a Simple Puzzle”
