Posts that are contributed to R-Bloggers
The Bundesliga is Germany’s primary football league. It is one of the most important football leagues in the world, broadcast on television in over 200 countries.
If you want to get your hands on a tool to forecast the result of any game (and perform some more statistical analyses), read on!
Continue reading “New Bundesliga Forecasting Tool: Can Underdog Hertha Berlin beat Bayern Munich?”
In view of the current dramatic events in Afghanistan many wonder why the extensive international efforts to bring some stability to the country have failed so miserably.
In this post, we will present and analytically examine a fascinating theory that seems to be able to explain political (in-)stability almost mono-causally, so read on!
Continue reading “The “Youth Bulge” of Afghanistan: The Hidden Force behind Political Instability”
Over the course of the last two and a half years, I have written over one hundred posts for my blog “Learning Machines” on the topics of data science, i.e. statistics, artificial intelligence, machine learning, and deep learning.
I use many of those in my university classes and in this post, I will give you the first part of a learning path for the knowledge that has accumulated on this blog over the years to become a well-rounded data scientist, so read on!
Continue reading “Learning Path for “Data Science with R” – Part I”
Everybody is talking about big data but the real skill lies in the art of inferring useful information from only a handful of values!
If you want to learn how to determine the range of the typical value of a dataset (i.e. the median) with just five values and why this works, read on!
Continue reading “The Small Data Rule: Infer the Big Picture from only Five Values!”
In this post, we will first give some intuition for and then demonstrate what is often called the most beautiful formula in mathematics, Euler’s identity, in R – first numerically with base R and then also symbolically, so read on!
Continue reading “Euler Coding Challenge: Build Maths’ Most Beautiful Formula in R”
One of the big sensations of the UEFA Euro 2020 is that Switzerland kicked out world champion France. We take this as an opportunity to share with you a simple statistical model to predict football (soccer) results with R, so read on!
Continue reading “Euro 2020: Will Switzerland kick out Spain too?”
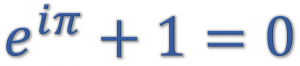
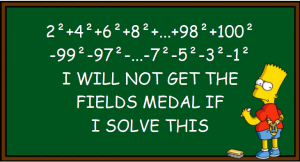This time we want to solve the following simple task with R: Take the numbers 1 to 100, square them, and add all the even numbers while subtracting the odd ones!
If you want to see how to do that in at least seven different ways in R, read on!
Continue reading “R Coding Challenge: 7 (+1) Ways to Solve a Simple Puzzle”
More and more decisions by banks on who gets a loan are being made by artificial intelligence. The terms being used are credit scoring and credit decisioning.
They base their decisions on models whether the customer will pay back the loan or will default, i.e. determine their creditworthiness. If you want to learn how to build such a model in R yourself (with the latest R ≥ 4.1.0 syntax as a bonus), read on!
Continue reading “Will I get my Money back? Credit Scoring with OneR”
Not many people understand the financial alchemy of modern financial investment vehicles, like hedge funds, that often use sophisticated trading strategies. But everybody understands the meaning of rising and falling markets. Why not simply translate one into the other?
If you want to get your hands on a simple R script that creates an easy-to-understand plot (a profit & loss profile or payoff diagram) out of any price series, read on!
Continue reading “Financial X-Rays: Dissect any Price Series with a simple Payoff Diagram”
Public-key cryptography is one of the foundations of our modern digital life. Normally it is quite hard to understand but with our literally colourful explanation it is a walk in the park. At the end we also give the nerd version, so read on!
Continue reading “Understanding Public-Key Cryptography by Mixing Colours!”
