
The 21st century has been marked by a series of global crises – from environmental degradation and pandemics to economic instability and political unrest.
As we hurtle forward towards the future, it’s becoming increasingly clear that the challenges we face as a species are numerous and interlinked, the word “polycrisis” is making the rounds.
These pressing issues raise the question: will humanity survive in the long term, or are we facing extinction – and if so, when? If you want to learn about a method to predict doomsday, read on!
My colleague Professor Richard Gott III from the elite university of Princeton has developed a simple mathematical model to answer this and many other questions that suffer from a high degree of uncertainty and published his research in the prestigious journal Nature.
The following post is based on “A math equation that predicts the end of humanity” by William Poundstone, who also wrote a whole book on the matter (“The Doomsday Calculation”).
You can also watch the video for this post (in German):
In 1969, Gott, a then recent Harvard physics graduate, was spending his summer in Europe. During a visit to the Berlin Wall, he made a quick calculation and informed his friend: “The Berlin Wall will last a minimum of 2 and 2/3 more years and a maximum of 24 more years.” The wall indeed came down 20 years later, in 1989! How on earth did he do the calculation and how can this method be used to calculate the arrival date of doomsday? It all boils down to something called the Copernican method!
The Copernican method, as described by Gott, is based on the Copernican principle originally introduced by Renaissance astronomer Copernicus. The principle states that the Earth is not the center of the universe and that humanity’s position in the universe is not special or central. It is widely accepted that our sun is an ordinary star in an ordinary galaxy, making humanity’s position in the universe unremarkable.
Gott applied this principle to time, rather than just space, meaning that when making the calculation we don’t occupy some special point in time. This can be demonstrated through a simple illustration where the existence of the Berlin Wall is represented as a bar, similar to a video timeline with a start, middle, and end.
Consider a tourist making the prediction that the future duration of the Berlin Wall will be between one-third and three times its past duration. If the wall is eight years old at the time of the prediction, the most likely future duration would be between 2.67 and 24 more years with a 50% chance of being correct (as an added bonus the following code allows you to create plots of this sort with all kinds of confidence intervals!):
gott_plot <- function(from = 25, to = 75, colour = "gray", left = "", right = "", middle = "Prediction will be\n true for all\n moments in\n this area", main = ""){
plot(c(0, 100), c(0, 1), type = "n", xlab = "", ylab = "", xaxt = "n", yaxt = "n", main = main)
axis(1, at = c(0, from, to, 100), labels = c("0%", paste0(from, "%"), paste0(to, "%"), "100%"))
rect(from, 0, to, 1, col = colour)
if (left != "") text(-1, 0.5, left, pos = 3, adj = 0, srt = 90)
if (right != "") text(103, 0.5, right, pos = 3, adj = 1, srt = 90)
if (middle != "") text((from + to) / 2, 0.5, middle, adj = 0.5, cex = 1.2)
}
gott_plot(colour = "red", left = "Berlin Wall built", right = "Berlin Wall demolished", main = "Berlin Wall's future duration from 1/3 to 3 times its past duration")
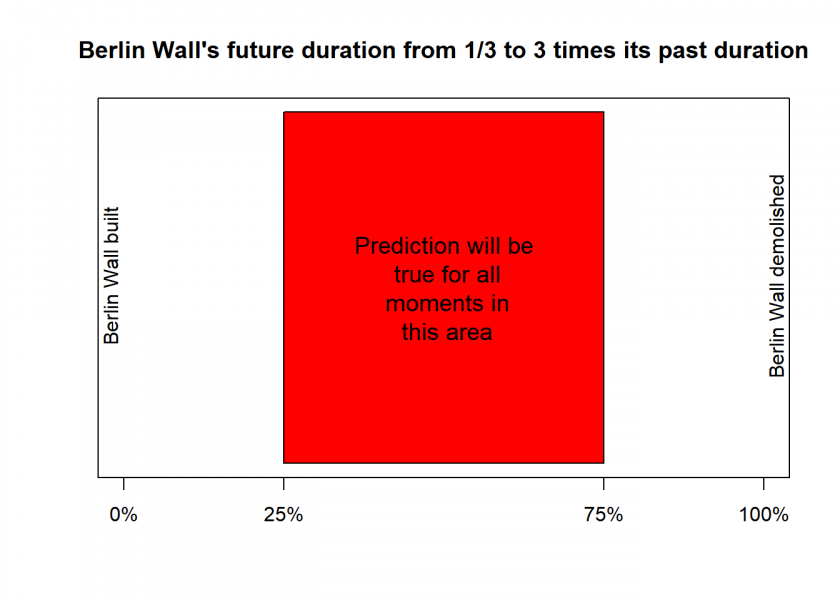
So, the Copernican method is a mathematical trick that makes predictions about the duration of an event based on its current age and the principle of randomness. The method involves creating a timeline of the event and marking a region, representing a desired level of confidence. The prediction about the future duration of the event is then made based on the length of the marked region.
Now, let us come to the question of when the world will end.
The human species has existed for around 200,000 years and has seen a significant increase in population in recent millennia. As a result, the chances of being alive in a time when there are more humans are higher. To reflect this, using human lives rather than years can provide a better understanding of time.
Imagine a list of every person who has or will ever live, sorted by birth date. Half of all humans will be in the first half of the list, and the other half will be in the second half. The position on this list determines the chances of future events, such as a decrease in the number of births compared to the past.
If we estimate the total number of people who have ever lived to be around 100 billion, then it can be estimated that there will be another 100 billion births within 760 years based on the current birth rate of 130 million per year. This means there is a 50% chance that humans will become extinct within 760 years, i.e. sometime around 2780:
gott_plot(from = 50, to = 100, colour = "red", left = "First humans", right = "Last humans", middle = "Prediction will be\n true for everyone\n in this part\n of the list", main = "No. of future births less than no. of past births")
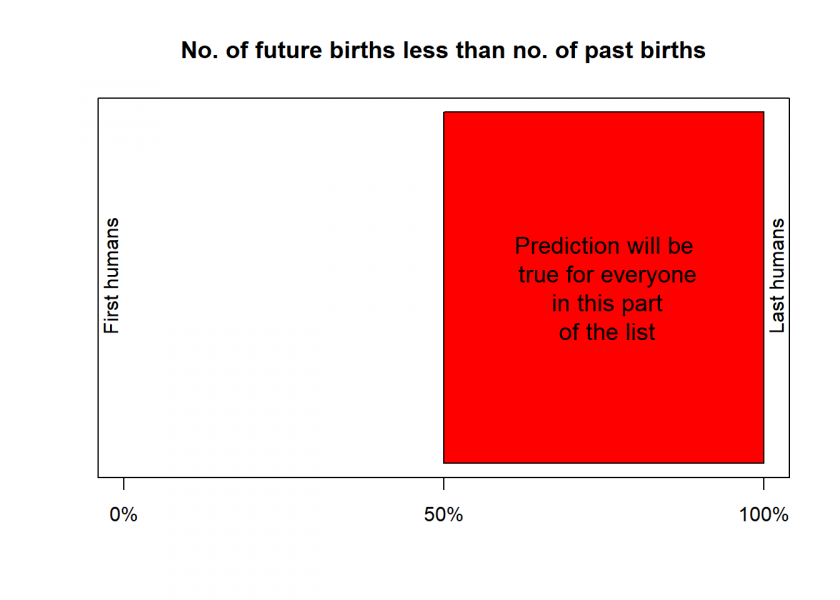
Although 760 years seems to be a lot it is next to nothing compared to the preceding 200,000 years. 760 years is only about 25 generations into the future compared to the ca. 6,700 generations before us. So, seen this way we are living in the end times of humanity. On the other hand, if this prediction proves to be false, Professor Gott won’t be around (one way or the other) to be blamed 😉
What do you think about this method? And what about the date it produces? Please write it in the comments below!

What if we have something not normally distributed?
Looking forward a Shiny calculator that includes non normal distributions:
https://github.com/WillKoehrsen/Data-Analysis/blob/master/copernican/Copernican%20Time%20Principle.ipynb