
This post presents a real highlight: We will build and backtest a quantitative trading strategy in R with the help of OpenAI’s ChatGPT-4! If you want to get a glimpse into the future of trading system development, read on!
On this blog, I already provided a template to build your own trading system (see Backtest Trading Strategies Like a Real Quant) but back in the days we did everything by hand. Not anymore! AI to the rescue! Also on this blog, we very early on did some coding experiments with ChatGPT (see ChatGPT can Create Datasets, Program in R… and when it makes an Error it can Fix that too!).
So now, I will present to you a full session with ChatGPT-4, including the used prompts, in which we build and backtest a trading strategy together, so buckle up!
You can also watch the video for this post (in German):
I tried different approaches and different prompts. As always with Large Language Models (LLMs) like ChatGPT you get the best results when you are as specific as possible. I also found out that it is best to give it some seed idea where to start, otherwise you will most often only end up with standard stuff like moving average crossovers or something like that. Because I am a big fan of risk-based investing, as I call it, I started with this prompt and had the following exchange with the AI (outputs of the code after running it are copied directly into the respective sections, both packages can be found on CRAN, if you want to run the code yourself):
You are a renowned quantitative finance investor. You want to create a new trading system. The idea is to have a long/flat strategy on the S&P 500 based on the volatility as a stress and risk indicator. Do everything step by step and explain your reasoning behind it. Be extra careful to avoid data snooping bias, survivorship bias, look ahead bias and overfitting. Use R for backtesting, but don’t use the tidyverse. Load the necessary data with the
quantmodpackage. The calculation of the performance and risk metrics should be done with thePerformanceAnalyticspackage. Give me the R code in one code window. I will give you the results of the tests and we will refine it together iteratively.
To create a long/flat trading system on the S&P 500 based on volatility, we’ll follow these steps:
- Load necessary libraries and data
- Calculate volatility as a risk indicator
- Develop the trading strategy
- Backtest the strategy
- Evaluate performance and risk metrics
Here is the R code to accomplish these tasks:
# Step 1: Load necessary libraries and data
library(quantmod)
library(PerformanceAnalytics)
start_date <- as.Date("2000-01-01")
end_date <- as.Date("2021-12-31")
symbol <- "^GSPC" # S&P 500 symbol
getSymbols(symbol, src = "yahoo", from = start_date, to = end_date)
price_data <- Ad(get(symbol))
# Step 2: Calculate volatility as a risk indicator
lookback_period <- 20
volatility <- runSD(ROC(price_data, n = 1, type = "discrete"), n = lookback_period) * sqrt(252)
# Step 3: Develop the trading strategy
threshold <- 0.15
signal <- ifelse(volatility < threshold, 1, 0)
signal <- lag(signal, 1) # To avoid look-ahead bias
signal[is.na(signal)] <- 0
# Step 4: Backtest the strategy
returns <- ROC(price_data, n = 1, type = "discrete") * signal
strategy_returns <- na.omit(returns)
# Step 5: Evaluate performance and risk metrics
charts.PerformanceSummary(strategy_returns, main = "Long/Flat Strategy based on Volatility")
table.AnnualizedReturns(strategy_returns)
maxDrawdown(strategy_returns)
Please run this R code, provide the results of the backtest, and we will refine the strategy iteratively based on the results.
It says "> price_data <- Ad(get(symbol))
Error in get(symbol) : object '^GSPC' not found"
Apologies for the confusion. It seems the variable name is causing issues. Let’s change the way we reference the data. Here’s the modified R code:
# Step 1: Load necessary libraries and data
library(quantmod)
library(PerformanceAnalytics)
start_date <- as.Date("2000-01-01")
end_date <- as.Date("2021-12-31")
symbol <- "^GSPC" # S&P 500 symbol
getSymbols(symbol, src = "yahoo", from = start_date, to = end_date)
price_data <- Ad(get(symbol))
# Step 2: Calculate volatility as a risk indicator
lookback_period <- 20
volatility <- runSD(ROC(price_data, n = 1, type = "discrete"), n = lookback_period) * sqrt(252)
# Step 3: Develop the trading strategy
threshold <- 0.15
signal <- ifelse(volatility < threshold, 1, 0)
signal <- lag(signal, 1) # To avoid look-ahead bias
signal[is.na(signal)] <- 0
# Step 4: Backtest the strategy
returns <- ROC(price_data, n = 1, type = "discrete") * signal
strategy_returns <- na.omit(returns)
# Step 5: Evaluate performance and risk metrics
charts.PerformanceSummary(strategy_returns, main = "Long/Flat Strategy based on Volatility")
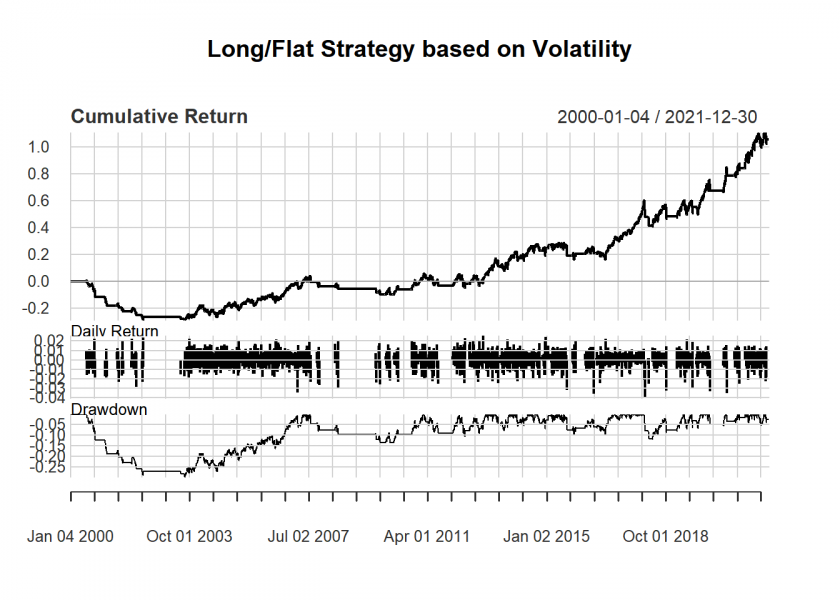
table.AnnualizedReturns(strategy_returns) ## GSPC.Adjusted ## Annualized Return 0.0334 ## Annualized Std Dev 0.0875 ## Annualized Sharpe (Rf=0%) 0.3821 maxDrawdown(strategy_returns) ## [1] 0.2954578
Please run this updated R code, and provide the results of the backtest. We will refine the strategy iteratively based on the results.
Please modify the code so that one can compare the strategy with the underlying benchmark
Sure, I have modified the code to include the benchmark (S&P 500) performance for comparison:
# Step 1: Load necessary libraries and data
library(quantmod)
library(PerformanceAnalytics)
start_date <- as.Date("2000-01-01")
end_date <- as.Date("2021-12-31")
symbol <- "^GSPC" # S&P 500 symbol
getSymbols(symbol, src = "yahoo", from = start_date, to = end_date, auto.assign = FALSE) -> sp500_data
price_data <- Ad(sp500_data)
# Step 2: Calculate volatility as a risk indicator
lookback_period <- 20
volatility <- runSD(ROC(price_data, n = 1, type = "discrete"), n = lookback_period) * sqrt(252)
# Step 3: Develop the trading strategy
threshold <- 0.15
signal <- ifelse(volatility < threshold, 1, 0)
signal <- lag(signal, 1) # To avoid look-ahead bias
signal[is.na(signal)] <- 0
# Step 4: Backtest the strategy
returns <- ROC(price_data, n = 1, type = "discrete") * signal
strategy_returns <- na.omit(returns)
# Calculate benchmark returns
benchmark_returns <- ROC(price_data, n = 1, type = "discrete")
benchmark_returns <- na.omit(benchmark_returns)
# Step 5: Evaluate performance and risk metrics
comparison <- cbind(strategy_returns, benchmark_returns)
colnames(comparison) <- c("Strategy", "Benchmark")
charts.PerformanceSummary(comparison, main = "Long/Flat Strategy vs S&P 500 Benchmark")
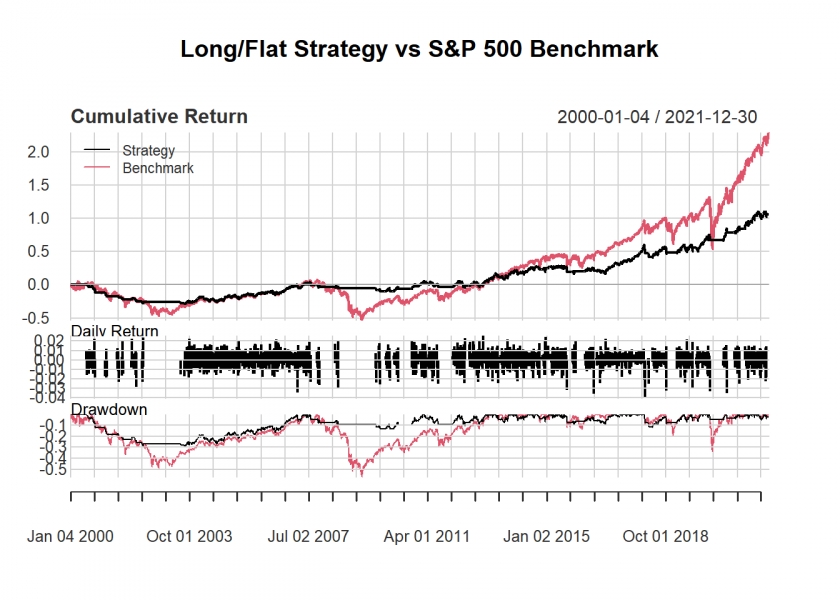
table.AnnualizedReturns(comparison) ## Strategy Benchmark ## Annualized Return 0.0334 0.0556 ## Annualized Std Dev 0.0875 0.1964 ## Annualized Sharpe (Rf=0%) 0.3821 0.2833 maxDrawdown(comparison) ## Strategy Benchmark ## Worst Drawdown 0.2954578 0.5677539
This code will plot the performance of both the long/flat strategy based on volatility and the S&P 500 benchmark, as well as display the annualized returns and maximum drawdown for each. Please run this updated R code and provide the results of the backtest. We will refine the strategy iteratively based on the results.
Here are the metrics:
table.AnnualizedReturns(comparison)
## Strategy Benchmark
## Annualized Return 0.0334 0.0556
## Annualized Std Dev 0.0875 0.1964
## Annualized Sharpe (Rf=0%) 0.3821 0.2833
maxDrawdown(comparison)
## Strategy Benchmark
## Worst Drawdown 0.2954578 0.5677539
Based on the metrics provided, the long/flat strategy has a lower annualized return (3.34%) compared to the S&P 500 benchmark (5.56%). However, the long/flat strategy has a lower annualized standard deviation (8.75%) than the benchmark (19.64%), indicating that it is less volatile. The Sharpe ratio (with risk-free rate = 0%) is higher for the long/flat strategy (0.3821) than the benchmark (0.2833), suggesting that the strategy has better risk-adjusted returns. Additionally, the maximum drawdown of the long/flat strategy (29.55%) is significantly lower than that of the benchmark (56.78%).
Depending on your investment objectives and risk tolerance, the long/flat strategy might be an attractive option due to its lower volatility and better risk-adjusted returns, despite having a lower annualized return compared to the S&P 500 benchmark.
If you would like to further refine the strategy, you may consider adjusting the lookback period, the volatility threshold, or incorporating additional indicators to improve the strategy’s performance. Please let me know if you’d like to explore further improvements or adjustments to the strategy.
How did you arrive at the lookback period (20) and the volatility threshhold (0.15)?
The lookback period of 20 and the volatility threshold of 0.15 were arbitrary choices for the initial version of the strategy. In practice, these parameters should be optimized to achieve better performance while ensuring the strategy remains robust and doesn’t overfit the data.
One approach to optimizing these parameters is to perform a parameter sweep, in which you systematically vary the lookback period and the volatility threshold within reasonable ranges and evaluate the strategy’s performance for each combination. This can help you identify the parameter combination that yields the best performance.
However, it’s important to avoid overfitting, which occurs when the strategy is tailored too closely to the historical data, leading to poor performance when applied to unseen data. To mitigate overfitting, you can use techniques like out-of-sample testing and cross-validation.
What could be the economic reason that this strategy outperforms the benchmark on a risk-adjusted basis?
The economic rationale behind the long/flat strategy outperforming the benchmark on a risk-adjusted basis can be attributed to the strategy’s ability to reduce exposure to market risk during periods of high volatility. High volatility is often associated with increased uncertainty, stress, and risk in financial markets. By going flat (i.e., not holding any position) during these periods, the strategy effectively manages risk and limits potential losses.
A few key points provide insights into why this approach works:
- Market inefficiencies: Financial markets are not always perfectly efficient. During periods of high volatility, market participants may react emotionally, leading to overreactions or panic selling. This can create price distortions and increase the risk of holding equities. By reducing exposure during high volatility, the long/flat strategy can avoid some of these potential losses.
- Risk aversion: When volatility is high, investors tend to become more risk-averse and prioritize preserving capital over seeking returns. This risk-averse behavior can lead to a preference for safer assets, causing a decline in equity prices. By going flat during these periods, the strategy aligns with the risk-averse behavior of market participants.
- Market turbulence: High volatility often indicates market turbulence or significant events (e.g., geopolitical risks, economic crises, or natural disasters) that can negatively impact the overall market or specific industries. By limiting exposure during periods of high volatility, the long/flat strategy helps mitigate the potential negative impact of such events.
- Diversification benefits: A long/flat strategy can provide diversification benefits to an investment portfolio. The strategy may exhibit low correlation with other assets or strategies, thereby enhancing the overall risk-adjusted performance of the portfolio.
By managing risk and reducing exposure during high-volatility periods, the long/flat strategy seeks to deliver better risk-adjusted returns compared to the benchmark. However, it’s important to keep in mind that past performance does not guarantee future results, and the strategy’s effectiveness may vary across different market conditions and time periods.
I could have gone on to further refine the strategy, optimize the parameters while avoiding overfitting, add more parameters, and so on, but this post is for illustrative purposes only. What I did though is to test the strategy out-of-sample for the year 2022 and Q1 2023. This is what I got:
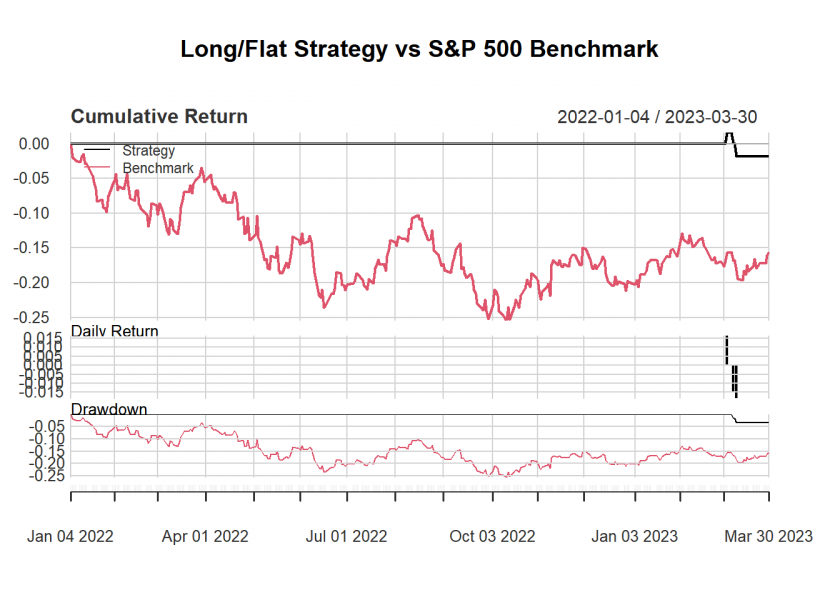
table.AnnualizedReturns(comparison) ## Strategy Benchmark ## Annualized Return -0.0145 -0.1280 ## Annualized Std Dev 0.0261 0.2294 ## Annualized Sharpe (Rf=0%) -0.5574 -0.5579 maxDrawdown(comparison) ## Strategy Benchmark ## Worst Drawdown 0.03350335 0.254251
I think the chart and the metrics speak for themselves! Quite impressive, don’t you think?
In the near future, it is conceivable that you can connect ChatGPT to R and the internet and everything would be done autonomously. There are already projects under way (e.g. “Auto-GPT”) that build the necessary infrastructure, so this will be only a matter of some short time horizon before we will have fully automated trading AIs in the markets (if they aren’t there already), constantly refining their strategies!
Please let me know your thoughts in the comments below!
DISCLAIMER
This post is written on an “as is” basis for educational purposes only, can contain errors, and comes without any warranty. The findings and interpretations are exclusively those of the author and are not endorsed by or affiliated with any third party.
In particular, this post provides no investment advice! No responsibility is taken whatsoever if you lose money.
(If you make any money though I would be happy if you would buy me a coffee… that is not too much to ask, is it? 😉 )

Fun! I hadn’t run much R for a while, hadn’t even installed it on my 2 year old laptop it seems, but I fired it up for this and enjoyed running the code a few times. I focused more on the 2011-date results. An interesting side note: running QQQ as the traded ETF with SPY as the benchmark used for volatility signals works significantly better than trading SPY with SPY signals. But… using QQQ volatility signals with trading QQQ seems not nearly as effective; not entirely intuitive why that might be. Look forward to followup posts about your ChatGPT + Finance coding adventures!
Thank you for your great feedback! The same: would love to hear about your experiences!
I love how you challenge conventional thinking and offer fresh ideas. It’s always exciting to read your blog.
Thank you very much for your feedback, ranit!
I think the simple beauty of this strategy is that it uses a volatility threshold to limit investing to low vol periods. By doing so, the strategy’s variance is only half that of its benchmark, opening possibilities for using leverage to improve returns. I reran this from 2000 using SPY (because you can buy SPY, but not ^GSPC), and instead of the “magical thinking” approach that this simple backtest uses (i.e., buying at the close if a signal is given using the value of that close) I chose to transact on the following day’s open. It gives very similar results as hoped, and expected, and is much easier to follow such a strategy. But then because the variance of this strategy is so low, I doubled the leverage by investing in SSO instead of SPY (and changed the dates to run from June of 2006, when SSO was introduced). The CAGR nearly doubled (beating SPY handily), the annualized standard deviation remained lower than the SD for SPY, the Sharpe was unchanged (again beating SPY), and the maximum drawdown was only half that for SPY. Additionally, the leveraged strategy ran ahead of the SPY strategy for ~90% of the time period. Thanks again for stimulating my return to R coding!
Wonderful! Thank you for sharing, Paul!