Learning R: The Collatz Conjecture


In this post, we will see that a little bit of simple R code can go a very long way! So let’s get started!

One of the fascinating features of number theory (unlike many other branches of mathematics) is that many statements are easy to make but the brightest minds are not able to prove them, the so-called Collatz conjecture (named after the German mathematician Lothar Collatz) is an especially fascinating example:

The Collatz conjecture states that when you start with any positive integer and

  • if it is even, the next number is one half the previous number and,
  • if it is odd, the next number is three times the previous number plus one

    • the sequence will always reach one.

It doesn’t get any simpler than that but no one has been able to prove this – and not for a lack of trying! The great mathematician Paul Erdős said about it “Mathematics may not be ready for such problems.” You can read more on Wikipedia: Collatz conjecture and watch an especially nice film that was made by a group of students:

So let us write a little program and try some numbers!

First we need a simple helper function to determine whether a number is even:

is.even <- function(x) {
  if (x %% 2 == 0) TRUE
  else FALSE
}

is.even(2)
## [1] TRUE

is.even(3)
## [1] FALSE

Normally we wouldn’t use a dot within function names but R itself (because of its legacy code) is not totally consistent here and the is-function family (like is.na or is.integer) all use a dot. After that we write a function for the rule itself, making use of the is.even function:

collatz <- function(n) {
  if (is.even(n)) n/2
  else 3 * n + 1
}

collatz(6)
## [1] 3

collatz(5)
## [1] 16

To try a number and plot it (like in the Wikipedia article) we could use a while-loop:

n_total <- n <- 27
while (n != 1) {
  n <- collatz(n)
  n_total <- c(n_total, n)
}

n_total
##   [1]   27   82   41  124   62   31   94   47  142   71  214  107  322  161
##  [15]  484  242  121  364  182   91  274  137  412  206  103  310  155  466
##  [29]  233  700  350  175  526  263  790  395 1186  593 1780  890  445 1336
##  [43]  668  334  167  502  251  754  377 1132  566  283  850  425 1276  638
##  [57]  319  958  479 1438  719 2158 1079 3238 1619 4858 2429 7288 3644 1822
##  [71]  911 2734 1367 4102 2051 6154 3077 9232 4616 2308 1154  577 1732  866
##  [85]  433 1300  650  325  976  488  244  122   61  184   92   46   23   70
##  [99]   35  106   53  160   80   40   20   10    5   16    8    4    2    1

plot(n_total, type = "l", col = "blue", xlab = "", ylab = "")

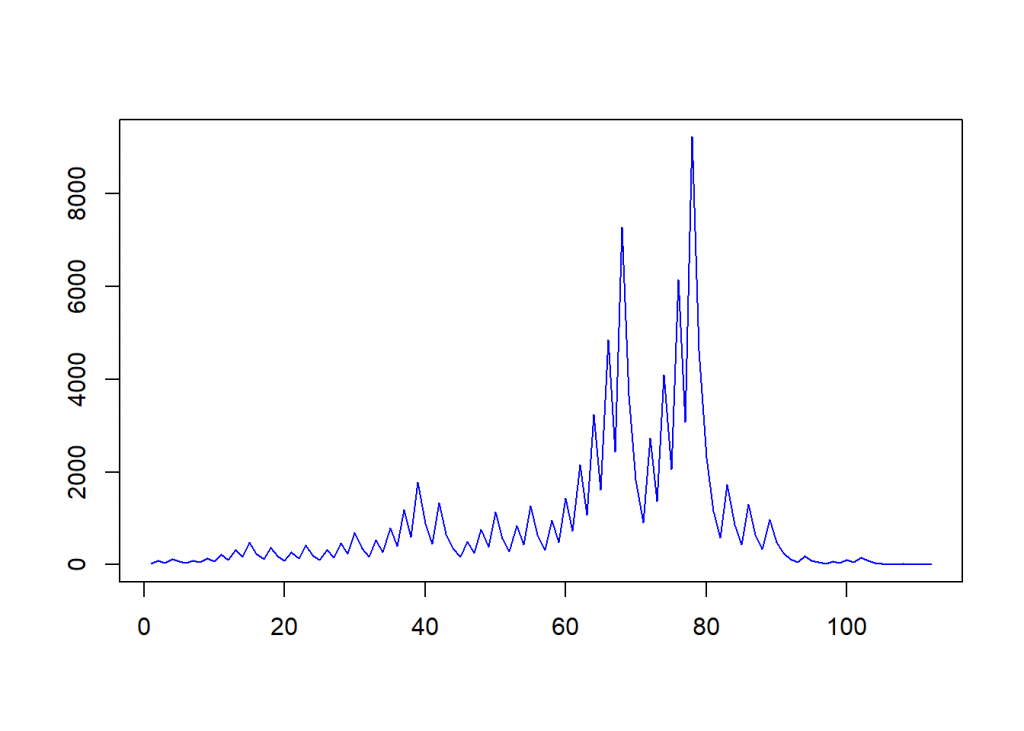
As you can see, after a wild ride the sequence finally reaches one as expected. We end with some nerd humour from the cult website xkcd:

Source: xkcd

8 thoughts on “Learning R: The Collatz Conjecture”

  3. Thank you very much for your post about Collatz Conjecture.
    I tried it in RStudio, and they all work successfully. What I learned from your programs that, to obtain a wonderful Collatz sequence, there are three steps to do:

    Step 1: Makes a function, which can determine a number even(gerade Zahl) or odd (ungerade Zahl). Here remainder operator ( %% ) and if (condition=TRUE)…(Output 1) else ..(Output 2) are applied.

    Step2: Applies Collatz Conjecture formula with determined number, to calculate the next number separately according to the Situation (parity). Continuing to use if…else, but the previous function is.even() as a condition I find a tricks!

    Step3: The last step is also the most crucial step. Because of this condition ‘n is not equal to 1’, this function completes all calculation of a serial number (that is sequence), which consists of themselves and their next neighbour in the Collatz Conjecture Formula till 1. The sticking Points are while-loop function which runs till the final number 1, and c() function to concatenate all the numbers into a sequence.

    The most interesting thing is the numver n itself.
    Whether it is even odd, big or small. Just like everyone of us, whether we are man or woman, level of social status or ability high or low. It is changing into another number, through getting and giving, like the energy or warm of the world. At the end, we give all back to our planet: the unique earth we live on. And each number is becoming from one, isn’t it? Every one (life) is an important part of this series of cycles. Each of us plays a role in society and returns to society.

    Thank you very much for your Inspiration for us.

    Reply

Leave a Reply

Your email address will not be published. Required fields are marked *

I accept that my given data and my IP address is sent to a server in the USA only for the purpose of spam prevention through the Akismet program.More information on Akismet and GDPR.

This site uses Akismet to reduce spam. Learn how your comment data is processed.