
Our intuition concerning randomness is, strangely enough, quite limited. While we expect it to behave in certain ways (which it doesn’t) it shows some regularities that have unexpected consequences. In a series of seemingly random posts, I will highlight some of those regularities as well as consequences. If you want to learn something about randomness’ strange behaviour and gain some intuition read on!
When Apple first introduced its shuffling function on the iPod customers were irritated and complained that it was not truly random. Oftentimes some titles appeared to be repeated too often while others seemed to have disappeared completely. What was going on?
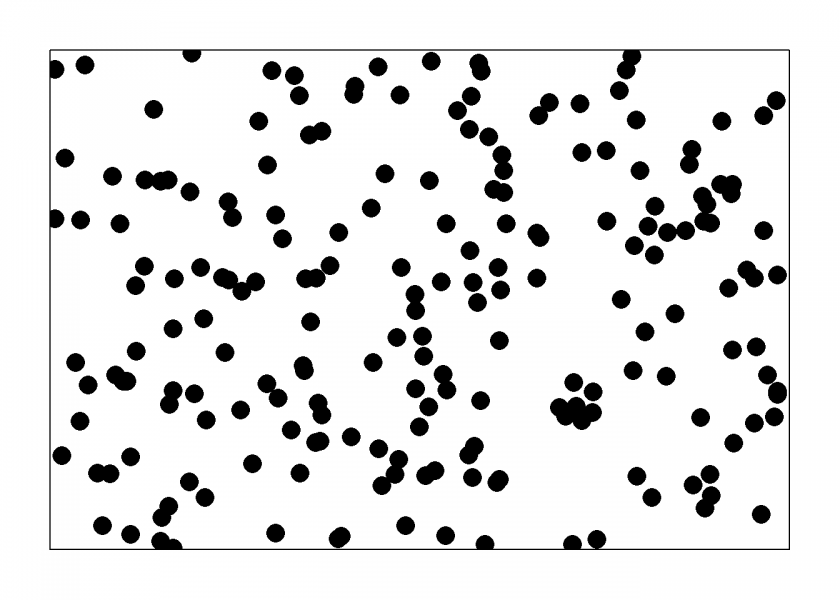
To illustrate the point I sometimes show my students the following two pics and ask them which was generated by randomness and which by an deterministic rule (you find the used randtoolbox package on CRAN):
library(randtoolbox)
## Loading required package: rngWELL
## This is randtoolbox. For an overview, type 'help("randtoolbox")'.
n <- 200
set.seed(2345)
x <- runif(n)
y <- runif(n)
oldpar = par(mar=c(2, 2, 2, 2) + 0.1)
plot(x, y, ylim = c(0, 1), xlim = c(0, 1), xaxs = "i", yaxs = "i", axes = FALSE, frame.plot = TRUE, pch = 16, cex = 2.1)
s <- sobol(n, 2, scrambling = 3) plot(s, ylim = c(0, 1), xlim = c(0, 1), xaxs = "i", yaxs = "i", axes = FALSE, frame.plot = TRUE, pch = 16, cex = 2.1)

Many a student thinks that the first pic was created by some underlying pattern (because of its points clumping together in some areas while leaving others empty) and that the second one is “more” random. The truth is that technically both are not random (but only pseudo-random) but the first resembles “true” randomness more closely while the second is a low-discrepancy sequence.
While coming to the point of pseudo-randomness in a moment “true” randomness may appear to have a tendency to occur in clusters or clumps (technically called Poisson clumping). This is the effect seen (or shall I say heard) in the iPod shuffling function. Apple changed it to a more regular behaviour (in the spirit of the second picture)… which was then perceived to be more random (as with my students)!
Now imagine that the first pic represents some map showing, let’s say, leukaemia in children. Wouldn’t we want to know whether there is some underlying reason for those clusters?!? Now imagine that there is a nuclear power plant near one of the more prominent clusters… just by chance! Oh, dear! Of course, it could be the reason for the cancer cases but just by looking at the map no real conclusions can be drawn! The takeaway message is that randomness often seems to have more pronounced patterns than purely deterministic sequences.
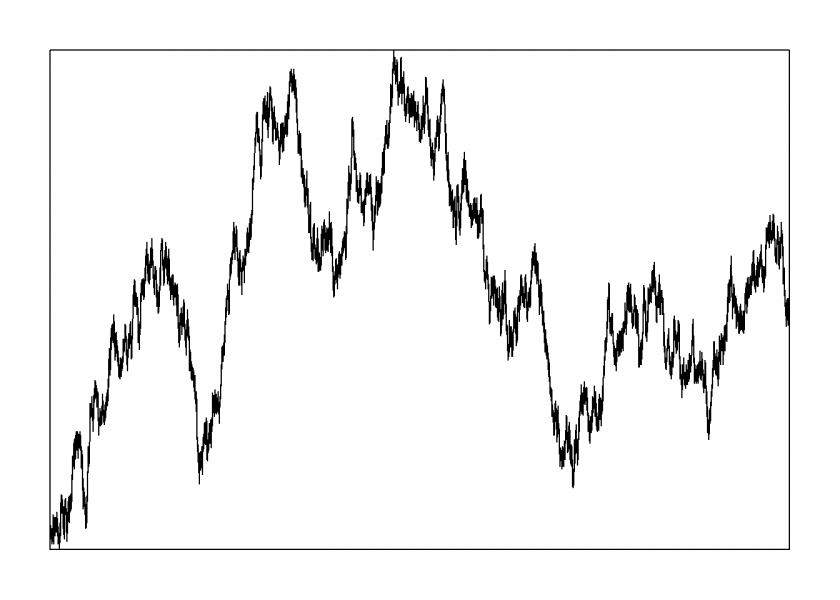
Another area where people are easily fooled by randomness is the stock market! Have a look at the following chart:
set.seed(3141) run <- sample(c(-1, 1), 1e5, replace = TRUE) plot(cumsum(run), type = "l", xaxs = "i", yaxs = "i", axes = FALSE, frame.plot = TRUE)
par(oldpar)
So-called technical analysts will clearly see what they call a Double Top pattern (basically the letter M in the chart) which they interpret as a bearish (= sell) signal. Now before you sell all of your stocks when you encounter something like this remember that the above chart was created purely by chance (as can be seen in the code)! Yet it seems as if all kinds of bullish and bearish trends can be observed.
Every quantitative analyst (or just quant) knows that stock charts (in most cases) cannot be distinguished from ones created by the toss of a coin. Yet we are evolutionarily trained to see all kinds of patterns, even when there are none. We see faces in fronts of cars and animals (or other funny things) in clouds… and buy and sell signals in random sequences.
While I will not get into the thorny (and philosophical) issue of what constitutes “true” randomness (perhaps some other time…) one thing is clear: computers are notoriously bad at creating it. Why? Because under the hood computers are purely deterministic animals, working on one command at a time. So they are only able to create something that looks like randomness: pseudo-randomness. On the positive side, that means that this kind of randomness is reproducible: in R you use the set.seed() function to get the same “random” sequence every time.
In the old days of computers (basically only a few decades ago) whole books with “good” random numbers were being published! The following can still be bought for over 50 bucks as a paperback and has over 600 pages! I guess it is the most unread book ever (even more than James Joyce’s Ulysses 😉 )
The following xkcd cartoon takes the idea of pseudo-randomness to its absurd extreme (as usual 🙂 ):



2 thoughts on “Learning Statistics: Randomness is a Strange Beast”