
One of the classic examples in data science (called data mining at the time) is the beer and diapers example: when a big supermarket chain started analyzing their sales data they encountered not only trivial patterns, like toothbrushes and toothpaste being bought together but also quite strange combinations like beer and diapers. Now, the trivial ones are reassuring that the method works but what about the more extravagant ones? Does it mean that young parents are alcoholics? Or that instead of breastfeeding they give their babies beer? Obviously, they had to get to the bottom of this.
As it turned out in many cases they following happened: stressed out mummy sends young daddy to the supermarket because they had run out of diapers. Young daddy seizes the opportunity to not only buy the much-needed diapers but also to stock up on some beer! So what the supermarket did was to place the beer directly on the way from the aisle with the diapers – the result was a significant boost in beer sales (for all the young daddies who might have forgotten what they really wanted when buying diapers…).
So, to reproduce this example in a simplified way have a look at the following code:
# some example data for items bought together (market baskets)
Diapers <- c(1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0)
Baby_Oil <- c(1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0)
Ham <- c(rep(0, 6), rep(1, 2), rep(0, 6), 1)
Beer <- c(rep(0, 3), 1, rep(0, 9), 1, 0)
(basket <- cbind(Diapers, Baby_Oil, Ham, Beer))
## Diapers Baby_Oil Ham Beer
## [1,] 1 1 0 0
## [2,] 0 1 0 0
## [3,] 1 1 0 0
## [4,] 1 0 0 1
## [5,] 0 0 0 0
## [6,] 1 1 0 0
## [7,] 1 0 1 0
## [8,] 0 0 1 0
## [9,] 1 1 0 0
## [10,] 1 1 0 0
## [11,] 0 1 0 0
## [12,] 0 1 0 0
## [13,] 1 1 0 0
## [14,] 1 1 0 1
## [15,] 0 0 1 0
# analysis of items bought together
round(cor_basket <- cor(basket), 2) # cor is the core of the method! (no pun intended)
## Diapers Baby_Oil Ham Beer
## Diapers 1.00 0.29 -0.27 0.32
## Baby_Oil 0.29 1.00 -0.71 -0.14
## Ham -0.27 -0.71 1.00 -0.20
## Beer 0.32 -0.14 -0.20 1.00
diag(cor_basket) <- 0 # we don't want to recommend the same products to the customers who already bought them
round(cor_basket, 2)
## Diapers Baby_Oil Ham Beer
## Diapers 0.00 0.29 -0.27 0.32
## Baby_Oil 0.29 0.00 -0.71 -0.14
## Ham -0.27 -0.71 0.00 -0.20
## Beer 0.32 -0.14 -0.20 0.00
# printing items bought together
for (i in 1:ncol(cor_basket)) {
col <- cor_basket[ , i]
col <- col[order(col, decreasing = TRUE)]
cat("Customers who bought", colnames(cor_basket)[i], "also bought", names(col)[col > 0], "\n")
}
## Customers who bought Diapers also bought Beer Baby_Oil
## Customers who bought Baby_Oil also bought Diapers
## Customers who bought Ham also bought
## Customers who bought Beer also bought Diapers
What we are looking for is some kind of dependance pattern within the shopping baskets, in this case we use the good old correlation function. Traditionally other (dependance) measures are used, namely support, confidence and lift. We will come to that later on in this post.
Wikipedia offers the following fitting description of association rule learning:
Association rule learning is a rule-based machine learning method for discovering interesting relations between variables in large databases. It is intended to identify rules discovered in databases using some measures of interestingness.
For example, the rule
found in the sales data of a supermarket would indicate that if a customer buys onions and potatoes together, they are likely to also buy hamburger meat.
Such information can be used as the basis for decisions about marketing activities such as e.g. promotional pricing or product placements.
In addition to the above example from market basket analysis association rules are employed today in many application areas including Web usage mining, intrusion detection, continuous production, and bioinformatics.
So, this is also the basis of popular functions on e-commerce sites (“customers who bought this item also bought…”) or movie streaming platforms (“customers who watched this film also watched…”).
Apropos films, I created a video for the first part of this post (in German):
A very good package for real-world datasets is the arules package (on CRAN). Have a look at the following code:
library(arules)
## Loading required package: Matrix
##
## Attaching package: 'arules'
## The following objects are masked from 'package:base':
##
## abbreviate, write
data("Groceries")
rules <- apriori(Groceries, parameter = list(supp = 0.001, conf = 0.5))
## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime support minlen
## 0.5 0.1 1 none FALSE TRUE 5 0.001 1
## maxlen target ext
## 10 rules FALSE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE 2 TRUE
##
## Absolute minimum support count: 9
##
## set item appearances ...[0 item(s)] done [0.00s].
## set transactions ...[169 item(s), 9835 transaction(s)] done [0.00s].
## sorting and recoding items ... [157 item(s)] done [0.00s].
## creating transaction tree ... done [0.00s].
## checking subsets of size 1 2 3 4 5 6 done [0.02s].
## writing ... [5668 rule(s)] done [0.00s].
## creating S4 object ... done [0.00s].
rules_conf <- arules::sort(rules, by = "confidence", decreasing = TRUE)
inspect(head(rules_conf, 10))
## lhs rhs support confidence lift count
## [1] {rice,
## sugar} => {whole milk} 0.001220132 1 3.913649 12
## [2] {canned fish,
## hygiene articles} => {whole milk} 0.001118454 1 3.913649 11
## [3] {root vegetables,
## butter,
## rice} => {whole milk} 0.001016777 1 3.913649 10
## [4] {root vegetables,
## whipped/sour cream,
## flour} => {whole milk} 0.001728521 1 3.913649 17
## [5] {butter,
## soft cheese,
## domestic eggs} => {whole milk} 0.001016777 1 3.913649 10
## [6] {citrus fruit,
## root vegetables,
## soft cheese} => {other vegetables} 0.001016777 1 5.168156 10
## [7] {pip fruit,
## butter,
## hygiene articles} => {whole milk} 0.001016777 1 3.913649 10
## [8] {root vegetables,
## whipped/sour cream,
## hygiene articles} => {whole milk} 0.001016777 1 3.913649 10
## [9] {pip fruit,
## root vegetables,
## hygiene articles} => {whole milk} 0.001016777 1 3.913649 10
## [10] {cream cheese ,
## domestic eggs,
## sugar} => {whole milk} 0.001118454 1 3.913649 1
The algorithm used here is the so-called Apriori algorithm. It ameliorates the problem with real-world datasets that when you want to test all combinations of all possible items you very soon run into performance problems – even with very fast computers – because there are just too many possibilities to be tested.
The Apriori algorithm aggressively prunes the possibilities to be tested by making use of the fact that if you are only interested in rules that are supported by a certain number of instances you can start with testing the support of individual items – which is easy to do – and work your way up to more complicated rules.
The trick is that you don’t test more complicated rules with items which don’t have enough support on the individual level: this is because if you don’t have enough instances on the individual level you don’t even have to look at more complicated combinations with those items included (which would be even more scarce). What sounds like an obvious point brings about huge time savings for real-world datasets which couldn’t be analyzed without this trick.
As mentioned above important concepts to assess the quality (or interestingness) of association rules are support, confidence and lift:
- Support of
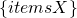 : percentage of X for all cases
: percentage of X for all cases - Confidence of
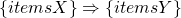 : percentage of Y for all X
: percentage of Y for all X - Lift of
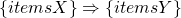 : ratio of the observed support of X and Y to what would be expected if X and Y were independent
: ratio of the observed support of X and Y to what would be expected if X and Y were independent
To understand these concepts better we are going to rebuild the examples given in the Wikipedia article in R. Have a look at the parts “Definition” and “Useful Concepts” of the article and after that at the following code, which should be self-explanatory:
M <- matrix(c(1, 1, 0, 0, 0,
0, 0, 1, 0, 0,
0, 0, 0, 1, 1,
1, 1, 1, 0, 0,
0, 1, 0, 0, 0), ncol = 5, byrow = TRUE)
colnames(M) <- c("milk", "bread", "butter", "beer", "diapers")
M
## milk bread butter beer diapers
## [1,] 1 1 0 0 0
## [2,] 0 0 1 0 0
## [3,] 0 0 0 1 1
## [4,] 1 1 1 0 0
## [5,] 0 1 0 0 0
supp <- function(X) {
sum(rowSums(M[ , X, drop = FALSE]) == length(X)) / nrow(M) # "rowSums == length" mimics logical AND for the selected columns
}
conf <- function(X, Y) {
supp(c(X, Y)) / supp(X) # conf(X => Y)
}
lift <- function(X, Y) {
supp(c(X, Y)) / (supp(X) * supp(Y)) # lift(X => Y)
}
supp(c("beer", "diapers")) # percentage of X for all cases
## [1] 0.2
conf(c("butter", "bread"), "milk") # percentage of Y for all X
## [1] 1
lift(c("milk", "bread"), "butter") # ratio of the observed support of X and Y to what would be expected if X and Y were independent
## [1] 1.25
You should conduct your own experiments by playing around with different item combinations so that you really understand the mechanics of those important concepts.
If all of those analyses are being done for perfecting your customer experience or just outright manipulation to lure you into buying stuff you don’t really need is obviously a matter of perspective…

2 thoughts on “Customers who bought…”