
Sorting values is one of the bread and butter tasks in computer science: this post uses it as a use case to learn what recursion is all about. It starts with some nerd humour… and ends with some more, so read on!
Have a look at the following code and try to understand it:
bogosort <- function(x) {
while(is.unsorted(x)) x <- sample(x)
x
}
set.seed(123)
(n <- sample(1:100, 10))
## [1] 29 79 41 86 91 5 50 83 51 42
bogosort(n)
## [1] 5 29 41 42 50 51 79 83 86 91
Obviously, bogosort did its job… but in a ludicrously inefficient way! It just shuffles all values over and over until they are sorted by chance! In the worst case, it just shuffles forever (i.e. until the sun swallows the earth or your partner switches the computer off… whatever comes first).
To create a more efficient sorting algorithm one could use the following strategy:
- Draw the smallest number, put it into a vector and
- Sort the remaining numbers by going back to 1.
The algorithm (which is called selection sort, see below) effectively sorts by calling itself! This is the main idea behind recursion.
To dive deeper into how recursion works watch the following video:
So, basically
Recursion means defining a function in terms of itself!
Additionally you need some stopping criterion or base case, otherwise you would create an infinite loop.
The recursive version of the factorial function is:
![]()
In the video this formula is written in C, here is the R version:
fact <- function(n) {
if (n == 1) 1
else n * fact(n-1)
}
fact(4)
## [1] 24
factorial(4) #inbuilt factorial function
## [1] 24
After we have seen how recursion actually works, let us implement the above selection sort algorithm in R. First watch this, admittedly unconventional, video:
So, the main idea behind the selection sort algorithm is to take the smallest number each time and add it to the sorted subset on the left. The sorting function calls itself for the unsorted subset on the right.
We now implement this idea recursively:
selsort <- function(x) {
if(length(x) > 1) {
mini <- which.min(x)
c(x[mini], selsort(x[-mini]))
} else x
}
set.seed(123)
(v <- sample(1:100, 20))
## [1] 29 79 41 86 91 5 50 83 51 42 87 98 60 94 9 77 21 4 27 78
selsort(v)
## [1] 4 5 9 21 27 29 41 42 50 51 60 77 78 79 83 86 87 91 94 98
Another, much more efficient sorting algorithm, quicksort, also works recursively. Watch the following video to get the idea:
So, the main idea behind the quicksort algorithm is to find a pivot for the unsorted set of numbers which splits it into two similarly sized subsets, on the left the numbers that are smaller than the pivot, on the right the numbers that are bigger. Then the sorting function calls itself for each subset.
Have a look at the following code:
qsort <- function(v) {
if (length(v) > 1) {
pivot <- (min(v) + max(v)) / 2
c(qsort(v[v < pivot]), v[v == pivot], qsort(v[v > pivot]))
} else v
}
qsort(v)
## [1] 4 5 9 21 27 29 41 42 50 51 60 77 78 79 83 86 87 91 94 98
Now for some speed comparisons between selection sort, quicksort and R’s sort function (on my lame computer…):
options(expressions = 7500) N <- 7000 set.seed(123) vs <- runif(N) system.time(u <- selsort(vs)) ## user system elapsed ## 0.59 0.14 0.73 system.time(u <- qsort(vs)) ## user system elapsed ## 0.01 0.00 0.01 system.time(u <- sort(vs)) ## user system elapsed ## 0 0 0
Wow, although quicksort was implemented in R (and not in C as the sort function) it is impressively fast. Why? Because each subset of unsorted numbers is again split into two subsets only about half as big. This pushes down the sizes of subsets that still have to be sorted down pretty fast. In the case of selection sort, the subset only gets smaller by one number (the smallest one) in each step.
Let us end this post with a little easter egg from Google – do you get it?
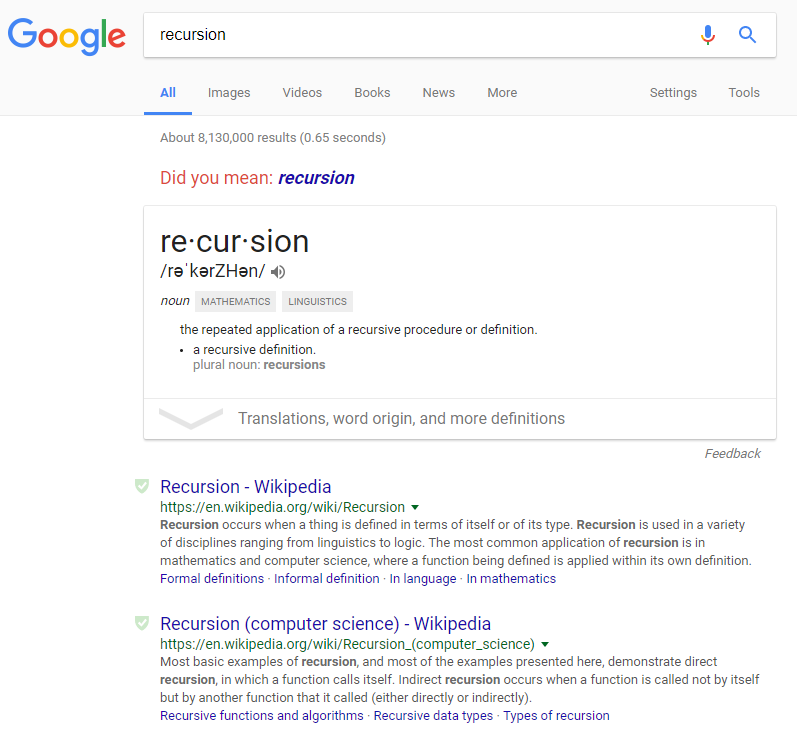

just keep in mind that recursion is useful in industrial work only if tail optimization is supported. otherwise your code will explode at some indeterminate time in the future. likely when the customer is doing some fabulously important and costly study.
Yes, indeed… that is the reason why I enhance the maximum number of nested expressions to 7,500 and sort only 7,000 numbers in the benchmark