
In data science, we try to find, sometimes well-hidden, patterns (= signal) in often seemingly random data (= noise). Pseudo-Random Number Generators (PRNG) try to do the opposite: hiding a deterministic data generating process (= signal) by making it look like randomness (= noise). If you want to understand some basics behind the scenes of this fascinating topic, read on!
In many an application, we rely on randomness. The problem is that a Turing machine, the theoretical foundation of every computer, knows no randomness. We need to create something that looks like randomness out of determinism. There are at least three questions hidden within:
- What is true randomness?
- What does “look like” mean in this context?
- Which data generating processes can be used in practice?
As you can imagine this is a huge topic and you can think about and do research on those topics for the rest of your remaining life. So, we leave number one to philosophy (and perhaps to a later post), will give a few hints on number two, and will foremost encounter a practical algorithm that is actually used to achieve number three and program it in R!
Normally users don’t think much about these topics but start to wonder what the set.seed() function is for. When I start to explain to my students that you can reproduce the exact same sequence of random numbers by setting a certain seed they mostly look at me as if I had lost my mind. The concept “exact same sequence of random numbers” just doesn’t make sense to them… and yet it is true:
set.seed(42); (u1 <- runif(30)) ## [1] 0.91480604 0.93707541 0.28613953 0.83044763 0.64174552 0.51909595 ## [7] 0.73658831 0.13466660 0.65699229 0.70506478 0.45774178 0.71911225 ## [13] 0.93467225 0.25542882 0.46229282 0.94001452 0.97822643 0.11748736 ## [19] 0.47499708 0.56033275 0.90403139 0.13871017 0.98889173 0.94666823 ## [25] 0.08243756 0.51421178 0.39020347 0.90573813 0.44696963 0.83600426 set.seed(42); (u2 <- runif(30)) ## [1] 0.91480604 0.93707541 0.28613953 0.83044763 0.64174552 0.51909595 ## [7] 0.73658831 0.13466660 0.65699229 0.70506478 0.45774178 0.71911225 ## [13] 0.93467225 0.25542882 0.46229282 0.94001452 0.97822643 0.11748736 ## [19] 0.47499708 0.56033275 0.90403139 0.13871017 0.98889173 0.94666823 ## [25] 0.08243756 0.51421178 0.39020347 0.90573813 0.44696963 0.83600426 identical(u1, u2) ## [1] TRUE
One way to illustrate this idea is to build a pseudorandom number generator (PRNG) ourselves. An especially simple one is a so-called Linear Congruential Generator (LCG). To generate a new random number you use this simple recurrence relation:
![]()
![]() is our new random number, which is created out of the random number before that
is our new random number, which is created out of the random number before that ![]() (or the seed to create the first random number).
(or the seed to create the first random number). ![]() ,
, ![]() and
and ![]() are predefined values and
are predefined values and ![]() is just the remainder of the division by
is just the remainder of the division by ![]() (
(%% in R).
The mathematical theory of how to choose good values for ![]() ,
, ![]() and
and ![]() is beyond this post. “Good” means that the generated random numbers actually “look” random. Some important criteria for that are:
is beyond this post. “Good” means that the generated random numbers actually “look” random. Some important criteria for that are:
- Uniformity of distribution for large quantities of generated numbers.
- Uncorrelatedness of successive values.
- No repetion of sequences of numbers.
Those are ideals no pseudorandom generator can reach but some are better than others in this regard. Ours is not particularly great but simple and relatively fast, so without further ado, we are going to build it in R. Actually we will build two different versions based on a task given by Rosetta Code, where I also posted my solution (for details see: Rosetta Code: Linear congruential generator). To be able to cope with very big integers that can occur during the intermediate steps of the calculation we use the gmp package (on CRAN):
library(gmp) # for big integers
##
## Attaching package: 'gmp'
## The following objects are masked from 'package:base':
##
## %*%, apply, crossprod, matrix, tcrossprod
rand_BSD <- function(n = 1) {
a <- as.bigz(1103515245)
c <- as.bigz(12345)
m <- as.bigz(2^31)
x <- rep(as.bigz(0), n)
x[1] <- (a * as.bigz(seed) + c) %% m
i <- 1
while (i < n) {
x[i+1] <- (a * x[i] + c) %% m
i <- i + 1
}
as.integer(x)
}
seed <- 0
rand_BSD(10)
## [1] 12345 1406932606 654583775 1449466924 229283573 1109335178
## [7] 1051550459 1293799192 794471793 551188310
rand_MS <- function(n = 1) {
a <- as.bigz(214013)
c <- as.bigz(2531011)
m <- as.bigz(2^31)
x <- rep(as.bigz(0), n)
x[1] <- (a * as.bigz(seed) + c) %% m
i <- 1
while (i < n) {
x[i+1] <- (a * x[i] + c) %% m
i <- i + 1
}
as.integer(x / 2^16)
}
seed <- 0
rand_MS(10)
## [1] 38 7719 21238 2437 8855 11797 8365 32285 10450 30612
In the second version (used by Microsoft) the results are divided by 65536 so that the created numbers lie in a range between 0 and 32767.
To create random numbers between 0 and 1 we just divide by 32767:
runif_MS <- function(n = 1) {
rand_MS(n) / 32767
}
boxplot(runif_MS(1000))
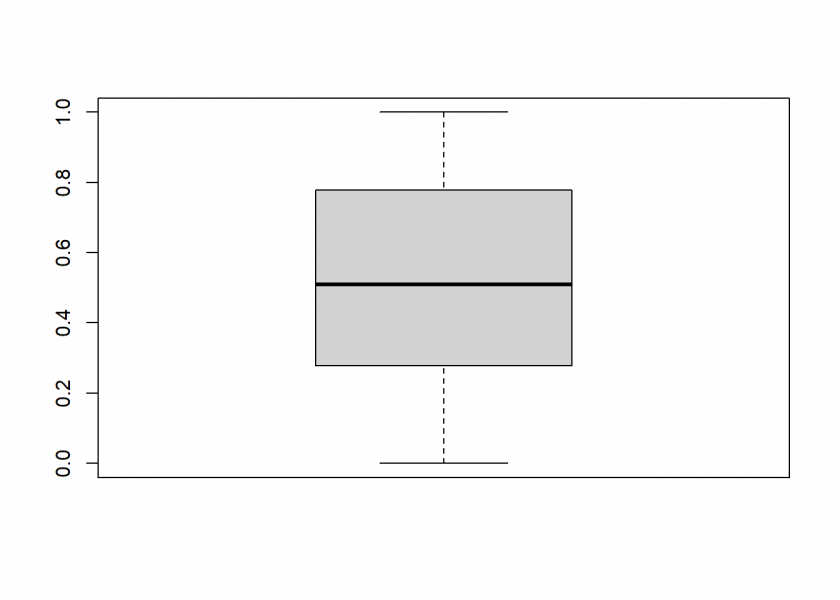
This seems to work pretty well. Sometimes we don’t want uniform random numbers but another distribution, most often normally distributed ones. The following illustration from Attilio Meucci’s excellent book “Risk and Asset Allocation” shows that this could easily be done by a mathematical transformation via the quantile function (here ![]() ) of the respective distribution:
) of the respective distribution:
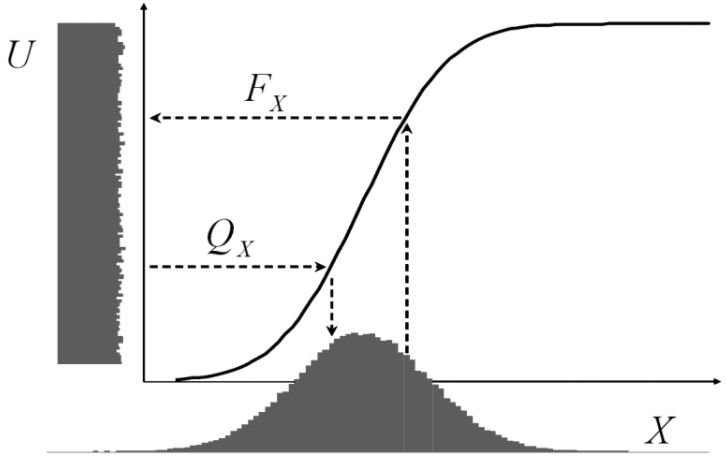
In R:
rnorm_MS <- function(n = 1) {
qnorm(runif_MS(n))
}
rand_NV <- rnorm_MS(2000)
hist(rand_NV)
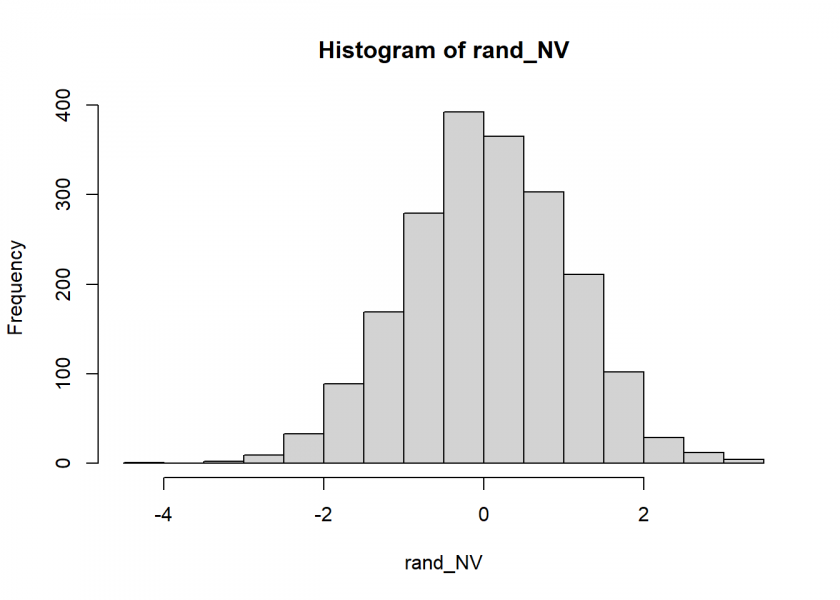
Not too bad… the Q-Q Plot, which compares the generates numbers to the real normal distribution, corroborates this:
qqnorm(rand_NV)
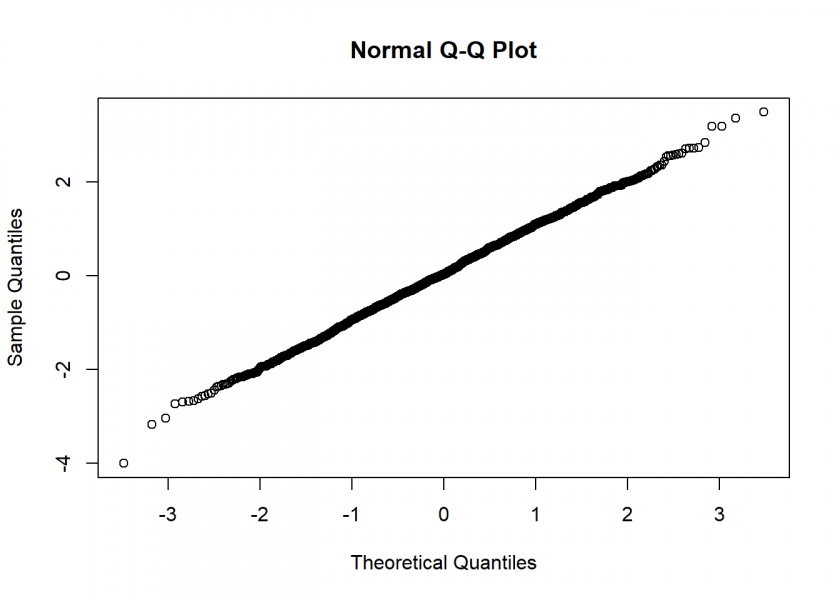
I hope you enjoyed our little journey from determinism via uniform to normally distributed (pseudo-)random numbers… in case you are still thinking about the question at the beginning (What is true randomness?), I have something for you to end this post:


Under the hood, rejection sampling is the technique used to generate random numbers from a uniform set that correspond to a particular distribution.
While implementing this manually is “overkill” when it comes to simpler distributions, i.e. normal, it can make sense when the distribution is overly complex.
Here is a recent article on the use of Rejection Sampling within Python: https://towardsdatascience.com/rejection-sampling-with-python-d7a30cfc327b
Thank you, Michael!
It says “You’ve read all your free member-only stories.” in my case… how about creating a (perhaps updated) R version of the article as a guest post here? Or perhaps another topic you see fit…
I’m terribly sorry about that – I didn’t realise there would be an issue in accessing the article.
Here is a separate version that I host on my own site: https://www.michael-grogan.com/articles/rejection-sampling-python
Certainly, a follow-up on Rejection Sampling in R would be quite useful – I will research this further and let you know!
Best,
Michael
Great, looking forward to it!
Following on from my previous post, here is an overview of Rejection Sampling with R using the AR package: https://www.michael-grogan.com/articles/rejection-sampling-r
Hope you find it useful!
Very useful indeed, thank you for sharing, Michael!