
Last week, I showed you a method of how to find the fastest path from A to B: Finding the Shortest Path with Dijkstra’s Algorithm. To make use of that, we need a method to determine our position at any point in time.
For that matter, many devices use the so-called Global Positioning System (GPS). If you want to understand how it works and do some simple calculations in R, read on!
Nowadays most of us have several GPS devices, in their cars, their smartphones, and their smartwatches. Those are receivers of signals coming from over 30 satellites orbiting the earth. You need that many so that there are always enough in sight:
Many of the technical details are interesting, yet here I want you to understand the core principle of how it works. With the real GPS, you need three satellites to determine two coordinates one of which can be discarded. Because the clock in the GPS receiver is not fully synchronized you need a fourth satellite to compensate for that. The resulting system of equations has to be solved to determine the position. In our toy example, we will only do the 2D-case with two satellites, yet the principle stays the same.
The following example is taken from the excellent article From Barns to Satellites: An Introduction to the Mathematics of Global Positioning Systems by my colleague Professor Kyle Schultz from the University of Mary Washington.
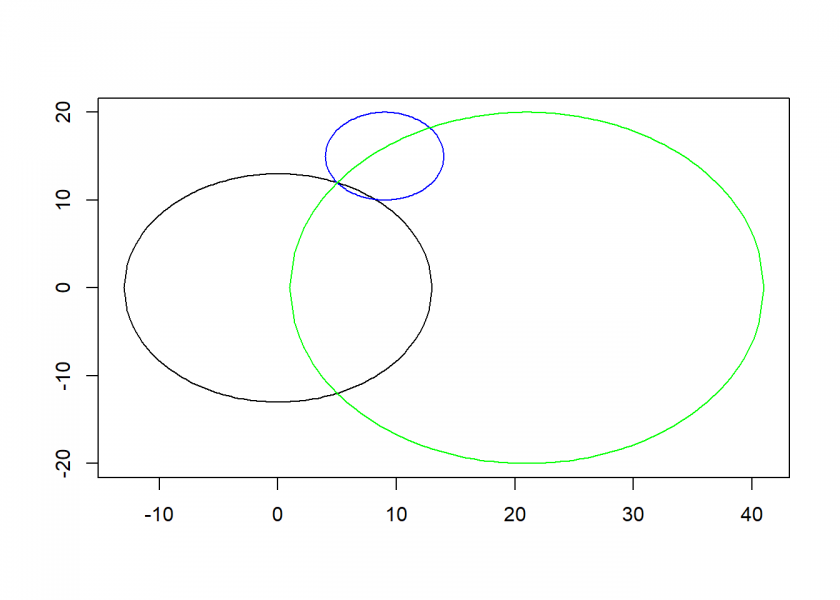
The basic principle of determining the position is finding the intersection of the two circles of the two satellites (in this case) and matching this with a third circle, given by the radius of the earth. We get circles because when we receive the signal of a satellite we receive the time when it sent the signal and the position where it was when it sent the signal. From that, we can infer a circle of all the positions the signal could have traveled to during the time interval until we received it.
When we have two satellites we get two circles. Two circles have either no, one or two intersections. When the system is set up correctly we will have two intersections most of the time. One of those can in nearly all cases be discarded because it will be somewhere in space or beneath the earth (x and y are the coordinates, r is the radius of the circle):
draw_circle <- function(x = 0, y = 0, r, xlim = NULL, ylim = NULL, col = "black", add = FALSE) {
h <- x
k <- y
if (is.null(ylim)) ylim <- c(k - r, k + r)
curve(+ sqrt(r^2 - (x - h)^2) + k, h - r, h + r, xlim = xlim, ylim = ylim, xlab = "", ylab = "", col = col, add = add)
curve(- sqrt(r^2 - (x - h)^2) + k, h - r, h + r, xlim = xlim, ylim = ylim, xlab = "", ylab = "", col = col, add = TRUE)
}
earth <- c(x = 0, y = 0, r = 13) # earth
sat_1 <- c(x = 21, y = 0, r = 20) # satellite 1
sat_2 <- c(x = 9, y = 15, r = 5) # satellite 2
draw_circle(r = earth["r"], xlim = c(-13, 41), ylim = c(-20, 20)) # earth
draw_circle(x = sat_1["x"], y = sat_1["y"], r = sat_1["r"], xlim = c(-13, 41), ylim = c(-20, 20), col = "green", add = TRUE) # satellite 1
draw_circle(x = sat_2["x"], y = sat_2["y"], r = sat_2["r"], ylim = c(-20, 20), col = "blue", add = TRUE) # satellite 2
The method for finding the intersection is called trilateration. You can find the exact mathematical derivation in the above article. We put the resulting formula into an R function (the d‘s stand for distances, the p, q and r for the coordinates of the satellites (we do not need the y-value of the first satellite because of the alignment of the diagram, see the article for details!):
trilaterate <- function(d1, d2, d3, p, q, r) {
x <- (p^2 + d1^2 - d2^2) / (2 * p)
y <- (q^2 + r^2 + d1^2 - d3^2 - (q * (p^2 + d1^2 - d2^2)) / p) / (2 * r)
return(c(x, y))
}
(P <- trilaterate(earth["r"], sat_1["r"], sat_2["r"], sat_1["x"], sat_2["x"], sat_2["y"])) # don't need sat_1["y"] because of alignment of satellites with earth
## x y
## 5 12
lines(c(earth["x"], P["x"]), c(earth["y"], P["y"]))
lines(c(sat_1["x"], P["x"]), c(sat_1["y"], P["y"]), col = "green")
lines(c(sat_2["x"], P["x"]), c(sat_2["y"], P["y"]), col = "blue")
points(P["x"], P["y"], pch = 16, col = "red")
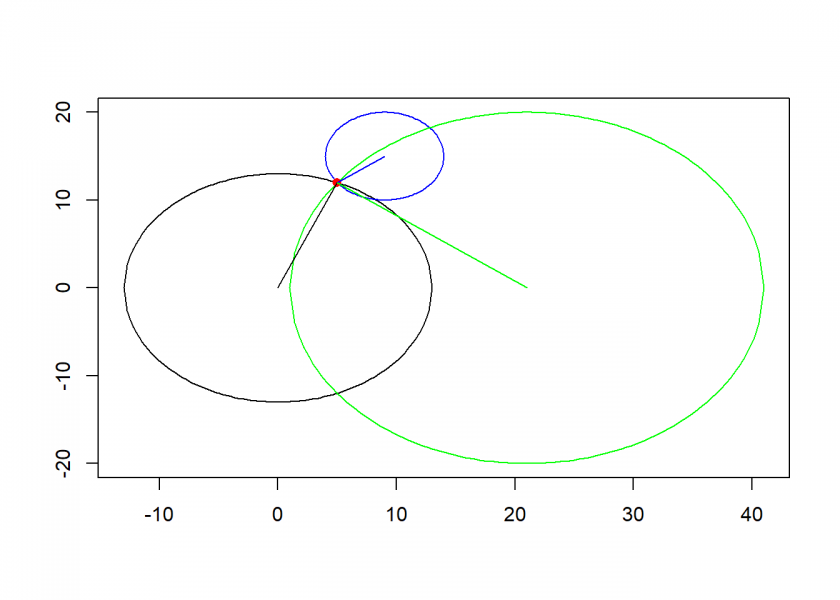
As you can see, we got a unique position (5, 12) by this method.

Another fascinating aspect of GPS is, that it is a practical application of Einstein’s Theory of Relativity! That is because the satellites are moving very fast in relation to the surface of the earth and gravity is much weaker up there! Both have to be incorporated into the equation, otherwise, we would have an accumulating error of more than 10 km per day! The system would obviously be totally useless without Einstein and his brilliant theory!

You can imagine what the pundits were saying about Einstein. 🙂
In 1905: “His theory [special relativity] will never have technological applications, nothing moves fast enough for these ‘corrections’ to make any difference.”
In 1915: “Practical significance of this general theory is even less than that of the previous, if it is even a correct one.”
Well, there may have been distinction between 1905 and 1915. Special relativity was partly known before Einstein, and he was probably the first to fully develop it by a margin of a few years. Its effects have to taken into account in great many applications involving electromagnetic waves, nuclear physics etc. General relativity (explanation of gravitational effects) is far more complex, and has few technological applications beyond satellites. Due to the lack of precision measurements, it had scientifically more or less equal competitors at the time of publication. From retrospect, it’s quite astonishing that the two theories were developed just ten years apart, and by the same person. And great luck that Einstein had strong scientific reputation by 1915, otherwise his general theory would probably have been totally dismissed!
Yes, that is true. A big plus was that his theories could still be tested, yet sometimes only decades later. The problem with modern theoretical physics is that we are more and more entering realms that cannot be tested properly. That makes progress so hard…