
Everybody and their dog are talking about ChatGPT from OpenAI. If you want to get an intuition about what lies at the core of such Language Models, read on!
Continue reading “Create Texts with a Markov Chain Text Generator… and what this has to do with ChatGPT!”
Category: Rosetta Code
Posts about code examples on Rosetta Code
Solving Einstein’s Puzzle with Constraint Programming

The following puzzle is a well-known meme in social networks. It is said to have been invented by young Einstein and back in the days I was ambitious enough to solve it by hand (you should try too!).
Yet, even simpler is to use Constraint Programming (CP). An excellent choice for doing that is MiniZinc, a free and open-source constraint modelling language. And the best thing is that you can control it by R! If you want to see how, read on!
Continue reading “Solving Einstein’s Puzzle with Constraint Programming”
Euler Coding Challenge: Build Maths’ Most Beautiful Formula in R
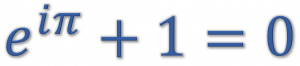
In this post, we will first give some intuition for and then demonstrate what is often called the most beautiful formula in mathematics, Euler’s identity, in R – first numerically with base R and then also symbolically, so read on!
Continue reading “Euler Coding Challenge: Build Maths’ Most Beautiful Formula in R”
Learning R: Creating Truth Tables

A short one for today: in this post we will learn how to easily create truth tables with R and will contribute our code to the growing repository of Rosetta code. I hope that you will learn a few tricks along the way, so read on!
Continue reading “Learning R: Creating Truth Tables”
Pseudo-Randomness: Creating Fake Noise

In data science, we try to find, sometimes well-hidden, patterns (= signal) in often seemingly random data (= noise). Pseudo-Random Number Generators (PRNG) try to do the opposite: hiding a deterministic data generating process (= signal) by making it look like randomness (= noise). If you want to understand some basics behind the scenes of this fascinating topic, read on!
Continue reading “Pseudo-Randomness: Creating Fake Noise”
Learning R: Christmas Coding Challenge

In this year’s end post I will give you a little programming challenge!
Everybody knows the Christmas song “The Twelve Days of Christmas”! Your task is to write an R script that creates the lyrics!
Continue reading “Learning R: Christmas Coding Challenge”
Learning R: Build a Password Generator

It is not easy to create secure passwords. The best way is to let a computer do it by randomly combining lower- and upper-case letters, digits and other printable characters.
If you want to learn how to write a small function to achieve that read on!
Continue reading “Learning R: Build a Password Generator”
Learning R: Painting with Fire

A few months ago I published a post on recursion: To understand Recursion you have to understand Recursion…. In this post we will see how to use recursion to fill free areas of an image with colour, the caveats of recursion and how to transform a recursive algorithm into a loop-based version using a queue – so read on…
Continue reading “Learning R: Painting with Fire”
Check Machin-like Formulae with Arbitrary-Precision Arithmetic
Happy New Year to all of you! Let us start the year with something for your inner maths nerd 🙂

Continue reading “Check Machin-like Formulae with Arbitrary-Precision Arithmetic”
