
We already saw the power of the OneR package in the preceding post, One Rule (OneR) Machine Learning Classification in under One Minute. Here we want to give some more examples to gain some fascinating, often counter-intuitive, insights.
Shirin Glander of Muenster University tested the OneR package with data from the World Happiness Report to find out what makes people happy: https://shiring.github.io/machine_learning/2017/04/23/one_r.
The whole analysis is very sophisticated so I present a simplified approach here. Have a look at the following code:
library(OneR)
data <- read.csv("data/2016.csv", sep = ",", header = TRUE)
data$Happiness.Score <- bin(data$Happiness.Score, nbins = 3, labels = c("low", "middle", "high"), method = "content")
data <- maxlevels(data) # removes all columns that have more than 20 levels (Country)
data <- optbin(formula = Happiness.Score ~., data = data, method = "infogain")
data <- data[ , -(1:4)] # remove columns with redundant data
model <- OneR(formula = Happiness.Score ~., data = data, verbose = TRUE)
##
## Attribute Accuracy
## 1 * Economy..GDP.per.Capita. 71.97%
## 2 Health..Life.Expectancy. 70.06%
## 3 Family 65.61%
## 4 Dystopia.Residual 59.87%
## 5 Freedom 57.32%
## 6 Trust..Government.Corruption. 55.41%
## 7 Generosity 47.13%
## ---
## Chosen attribute due to accuracy
## and ties method (if applicable): '*'
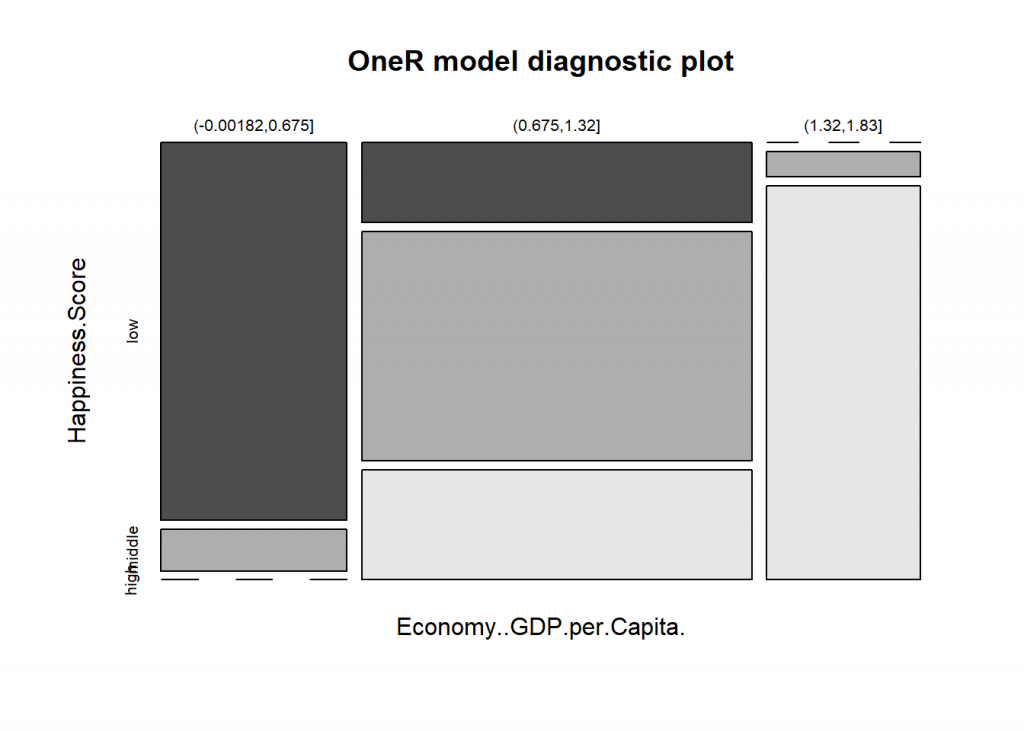
summary(model) ## ## Call: ## OneR.formula(formula = Happiness.Score ~ ., data = data, verbose = TRUE) ## ## Rules: ## If Economy..GDP.per.Capita. = (-0.00182,0.675] then Happiness.Score = low ## If Economy..GDP.per.Capita. = (0.675,1.32] then Happiness.Score = middle ## If Economy..GDP.per.Capita. = (1.32,1.83] then Happiness.Score = high ## ## Accuracy: ## 113 of 157 instances classified correctly (71.97%) ## ## Contingency table: ## Economy..GDP.per.Capita. ## Happiness.Score (-0.00182,0.675] (0.675,1.32] (1.32,1.83] Sum ## low * 36 16 0 52 ## middle 4 * 46 2 52 ## high 0 22 * 31 53 ## Sum 40 84 33 157 ## --- ## Maximum in each column: '*' ## ## Pearson's Chi-squared test: ## X-squared = 130.99, df = 4, p-value < 2.2e-16
plot(model)
prediction <- predict(model, data) eval_model(prediction, data) ## ## Confusion matrix (absolute): ## Actual ## Prediction high low middle Sum ## high 31 0 2 33 ## low 0 36 4 40 ## middle 22 16 46 84 ## Sum 53 52 52 157 ## ## Confusion matrix (relative): ## Actual ## Prediction high low middle Sum ## high 0.20 0.00 0.01 0.21 ## low 0.00 0.23 0.03 0.25 ## middle 0.14 0.10 0.29 0.54 ## Sum 0.34 0.33 0.33 1.00 ## ## Accuracy: ## 0.7197 (113/157) ## ## Error rate: ## 0.2803 (44/157) ## ## Error rate reduction (vs. base rate): ## 0.5769 (p-value < 2.2e-16)
As you can see we get more than 70% accuracy with three rules based on GDP per capita. So it seems that money CAN buy happiness after all!
Dr. Glander comes to the following conclusion:
All in all, based on this example, I would confirm that OneR models do indeed produce sufficiently accurate models for setting a good baseline. OneR was definitely faster than random forest, gradient boosting and neural nets. However, the latter were more complex models and included cross-validation.
If you prefer an easy to understand model that is very simple, OneR is a very good way to go. You could also use it as a starting point for developing more complex models with improved accuracy.
When looking at feature importance across models, the feature OneR chose – Economy/GDP per capita – was confirmed by random forest, gradient boosting trees and neural networks as being the most important feature. This is in itself an interesting conclusion! Of course, this correlation does not tell us that there is a direct causal relationship between money and happiness, but we can say that a country’s economy is the best individual predictor for how happy people tend to be.
A well known reference data set is the titanic data set which gives all kind of additional information on the passengers of the titanic and whether they survived the tragedy. We can conveniently use the titanic package from CRAN to get access to the data set. Have a look at the following code:
library(titanic) data <- bin(maxlevels(titanic_train), na.omit = FALSE) model <- OneR(Survived ~., data = data, verbose = TRUE) ## Warning in OneR.data.frame(x = data, ties.method = ties.method, verbose = ## verbose, : data contains unused factor levels ## ## Attribute Accuracy ## 1 * Sex 78.68% ## 2 Pclass 67.9% ## 3 Fare 64.42% ## 4 Embarked 63.86% ## 5 Age 62.74% ## 6 Parch 61.73% ## 7 PassengerId 61.62% ## 7 SibSp 61.62% ## --- ## Chosen attribute due to accuracy ## and ties method (if applicable): '*'
summary(model) ## ## Call: ## OneR.formula(formula = Survived ~ ., data = data, verbose = TRUE) ## ## Rules: ## If Sex = female then Survived = 1 ## If Sex = male then Survived = 0 ## ## Accuracy: ## 701 of 891 instances classified correctly (78.68%) ## ## Contingency table: ## Sex ## Survived female male Sum ## 0 81 * 468 549 ## 1 * 233 109 342 ## Sum 314 577 891 ## --- ## Maximum in each column: '*' ## ## Pearson's Chi-squared test: ## X-squared = 260.72, df = 1, p-value < 2.2e-16
plot(model)

prediction <- predict(model, data) eval_model(prediction, data$Survived) ## ## Confusion matrix (absolute): ## Actual ## Prediction 0 1 Sum ## 0 468 109 577 ## 1 81 233 314 ## Sum 549 342 891 ## ## Confusion matrix (relative): ## Actual ## Prediction 0 1 Sum ## 0 0.53 0.12 0.65 ## 1 0.09 0.26 0.35 ## Sum 0.62 0.38 1.00 ## ## Accuracy: ## 0.7868 (701/891) ## ## Error rate: ## 0.2132 (190/891) ## ## Error rate reduction (vs. base rate): ## 0.4444 (p-value < 2.2e-16)
So, somewhat contrary to popular belief, it were not necessarily the rich that survived but the women!
A more challenging data set is one about the quality of red wine (https://archive.ics.uci.edu/ml/datasets/Wine+Quality), have a look at the following code:
data <- read.csv("data/winequality-red.csv", header = TRUE, sep = ";")
data <- optbin(data, method = "infogain")
## Warning in optbin.data.frame(data, method = "infogain"): target is numeric
model <- OneR(data, verbose = TRUE)
##
## Attribute Accuracy
## 1 * alcohol 56.1%
## 2 sulphates 51.22%
## 3 volatile.acidity 50.59%
## 4 total.sulfur.dioxide 48.78%
## 5 density 47.22%
## 6 citric.acid 46.72%
## 7 chlorides 46.47%
## 8 free.sulfur.dioxide 44.47%
## 9 fixed.acidity 43.96%
## 10 residual.sugar 43.46%
## 11 pH 43.21%
## ---
## Chosen attribute due to accuracy
## and ties method (if applicable): '*'
summary(model) ## ## Call: ## OneR.data.frame(x = data, verbose = TRUE) ## ## Rules: ## If alcohol = (8.39,8.45] then quality = 3 ## If alcohol = (8.45,10] then quality = 5 ## If alcohol = (10,11] then quality = 6 ## If alcohol = (11,12.5] then quality = 6 ## If alcohol = (12.5,14.9] then quality = 6 ## ## Accuracy: ## 897 of 1599 instances classified correctly (56.1%) ## ## Contingency table: ## alcohol ## quality (8.39,8.45] (8.45,10] (10,11] (11,12.5] (12.5,14.9] Sum ## 3 * 1 5 4 0 0 10 ## 4 0 28 13 11 1 53 ## 5 0 * 475 156 41 9 681 ## 6 1 216 * 216 * 176 * 29 638 ## 7 0 19 53 104 23 199 ## 8 0 2 2 6 8 18 ## Sum 2 745 444 338 70 1599 ## --- ## Maximum in each column: '*' ## ## Pearson's Chi-squared test: ## X-squared = 546.64, df = 20, p-value < 2.2e-16
prediction <- predict(model, data) eval_model(prediction, data, zero.print = ".") ## ## Confusion matrix (absolute): ## Actual ## Prediction 3 4 5 6 7 8 Sum ## 3 1 . . 1 . . 2 ## 4 . . . . . . . ## 5 5 28 475 216 19 2 745 ## 6 4 25 206 421 180 16 852 ## 7 . . . . . . . ## 8 . . . . . . . ## Sum 10 53 681 638 199 18 1599 ## ## Confusion matrix (relative): ## Actual ## Prediction 3 4 5 6 7 8 Sum ## 3 . . . . . . . ## 4 . . . . . . . ## 5 . 0.02 0.30 0.14 0.01 . 0.47 ## 6 . 0.02 0.13 0.26 0.11 0.01 0.53 ## 7 . . . . . . . ## 8 . . . . . . . ## Sum 0.01 0.03 0.43 0.40 0.12 0.01 1.00 ## ## Accuracy: ## 0.561 (897/1599) ## ## Error rate: ## 0.439 (702/1599) ## ## Error rate reduction (vs. base rate): ## 0.2353 (p-value < 2.2e-16)
That is an interesting result, isn’t it: the more alcohol the higher the perceived quality!
We end this post with an unconventional use case for OneR: finding the best move in a strategic game, i.e. tic-tac-toe. We use a dataset with all possible board configurations at the end of such games, have a look at the following code:
data <- read.csv("https://archive.ics.uci.edu/ml/machine-learning-databases/tic-tac-toe/tic-tac-toe.data", header = FALSE)
names(data) <- c("top-left-square", "top-middle-square", "top-right-square", "middle-left-square", "middle-middle-square", "middle-right-square", "bottom-left-square", "bottom-middle-square", "bottom-right-square", "Class")
model <- OneR(data, verbose = TRUE)
##
## Attribute Accuracy
## 1 * middle-middle-square 69.94%
## 2 top-left-square 65.34%
## 2 top-middle-square 65.34%
## 2 top-right-square 65.34%
## 2 middle-left-square 65.34%
## 2 middle-right-square 65.34%
## 2 bottom-left-square 65.34%
## 2 bottom-middle-square 65.34%
## 2 bottom-right-square 65.34%
## ---
## Chosen attribute due to accuracy
## and ties method (if applicable): '*'
summary(model) ## ## Call: ## OneR.data.frame(x = data, verbose = TRUE) ## ## Rules: ## If middle-middle-square = b then Class = positive ## If middle-middle-square = o then Class = negative ## If middle-middle-square = x then Class = positive ## ## Accuracy: ## 670 of 958 instances classified correctly (69.94%) ## ## Contingency table: ## middle-middle-square ## Class b o x Sum ## negative 48 * 192 92 332 ## positive * 112 148 * 366 626 ## Sum 160 340 458 958 ## --- ## Maximum in each column: '*' ## ## Pearson's Chi-squared test: ## X-squared = 115.91, df = 2, p-value < 2.2e-16
prediction <- predict(model, data) eval_model(prediction, data) ## ## Confusion matrix (absolute): ## Actual ## Prediction negative positive Sum ## negative 192 148 340 ## positive 140 478 618 ## Sum 332 626 958 ## ## Confusion matrix (relative): ## Actual ## Prediction negative positive Sum ## negative 0.20 0.15 0.35 ## positive 0.15 0.50 0.65 ## Sum 0.35 0.65 1.00 ## ## Accuracy: ## 0.6994 (670/958) ## ## Error rate: ## 0.3006 (288/958) ## ## Error rate reduction (vs. base rate): ## 0.1325 (p-value = 0.001427)
Perhaps it doesn’t come as a surprise that the middle-middle-square is strategically the most important one – but still it is encouraging to see that OneR comes to the same conclusion.

Thank a lot for this great package.
Any suggestions for visualizing a OneR decision tree object?
Thank you Shani, I really appreciate it!
Well, what do you mean by “decision tree object”? Because basically it is a one-level decision tree the
plotfunction might be the visualization you are looking for?If you have another idea, please share it with me… I am always open to suggestions for improving the package.