
We have already covered the backtesting of trading strategies in this blog (see Backtest Trading Strategies Like a Real Quant), so let us up the ante: if you want to learn how to backtest options strategies, read on!
Options trading strategies are strategies where you combine, often several, derivatives instruments to create a certain risk-return profile (more on that here: Financial Engineering: Static Replication of any Payoff Function). Often we want to know how those strategies would fare in the real world.
The problem is that real data on derivatives are hard to come by and/or very expensive. But we help ourselves with a very good proxy: implied volatility which is freely available for example for many indices. With that, we can use the good old Black-Scholes model to reasonably price options whose strikes are not too far away from the current price of the underlying.
My colleague Professor Michael Stutzer from the University of Colorado demonstrates this in his wonderful paper How Students Can Backtest Madoff’s Claims and we are going to replicate this with R (one of my postgraduate students, Niklas Paulson, was kind enough to update parts of the code which I had written some time ago).
To run the code yourself you would have to install the powerful packages Quandl, quantmod and PerformanceAnalytics (all on CRAN). Additionally, you would have to register at quandl.com to receive your own API key (I will not show mine here for obvious reasons).
library(Quandl)
## Loading required package: xts
## Loading required package: zoo
##
## Attaching package: 'zoo'
## The following objects are masked from 'package:base':
##
## as.Date, as.Date.numeric
library(quantmod)
## Loading required package: TTR
## Registered S3 method overwritten by 'quantmod':
## method from
## as.zoo.data.frame zoo
## Version 0.4-0 included new data defaults. See ?getSymbols.
library(PerformanceAnalytics)
##
## Attaching package: 'PerformanceAnalytics'
## The following object is masked from 'package:graphics':
##
## legend
# get your API key via free registration at quandl.com and insert here
Quandl.api_key("XXX")
As an example, the paper backtests the so-called split strike conversion strategy (also known as a “collar”) which was allegedly pursued by Bernie Madoff’s hedge fund. We will see that this strategy would have fared quite well but unfortunately, it later turned out that Madoff didn’t pursue this strategy after all but had built up a large Ponzi scheme (for more on that: How to Catch a Thief: Unmasking Madoff’s Ponzi Scheme with Benford’s Law).
Anyway, the strategy itself is quite interesting, it consists of
- the purchase of a group or basket of equity securities that are intended to highly correlate to the S&P 100 index,
- the sale of ”out-of-the-money” S&P 100 index call options in an equivalent contract value dollar amount to the basket of equity securities, and
- the purchase of an equivalent number of “out-of-the-money” S&P 100 Index put options
First we have to load all the necessary data and transform them as needed:
# set parameters for out-of-the-money options
X <- 0.04 # put 4% OOM
Y <- 0.02 # call 2% OOM
# calculate S_tp0 (S&P 100 beginning of the month) and S_tp1 (S&P 100 end of the month)
getSymbols("^OEX", from = "1990-11-01", to = "2008-11-30", periodicity = "monthly") # values for S_tp0 and S_tp1
## 'getSymbols' currently uses auto.assign=TRUE by default, but will
## use auto.assign=FALSE in 0.5-0. You will still be able to use
## 'loadSymbols' to automatically load data. getOption("getSymbols.env")
## and getOption("getSymbols.auto.assign") will still be checked for
## alternate defaults.
##
## This message is shown once per session and may be disabled by setting
## options("getSymbols.warning4.0"=FALSE). See ?getSymbols for details.
## [1] "^OEX"
S <- coredata(OEX[ , "OEX.Adjusted"])
S_tp0 <- S[-length(S)] # remove last value -> November is only necessary as S_tp1 for October
S_tp1 <- S[-1] # remove first value -> starting value of S_tp1 is equal to the end value of S_tp0
# calculate monthly sigma_t (Volatility)
getSymbols("^VXO", from = "1990-11-01", to = "2008-10-31", periodicity = "monthly") # Values for implied volatility
## [1] "^VXO"
sigma_t <- coredata(VXO[ , "VXO.Adjusted"]) / 100
# calculate values for r_t, see also note 5 on p. 13
yield_t <- Quandl("FRED/TB3MS", trim_start = "1990-11-01", trim_end = "2008-10-31", order = "asc")
yield_t <- yield_t[ , "Value"] / 100
P_t <- 100 * (1 - 91/360 * yield_t)
r_t <- 4 * log(100/P_t)
We now define the functions for the payoffs of the puts and calls as stated on page 6 of the paper…
Put_t <- function(S_tp0, X, r_t, sigma_t) {
d1 <- (log(1/(1-X)) + (r_t + sigma_t^2/2) * 1/12) / (sigma_t*sqrt(1/12))
d2 <- d1 - sigma_t * sqrt(1/12)
(1-X) * S_tp0 * exp(-r_t/12) * pnorm(-d2) - S_tp0 * pnorm(-d1) # pnorm is cumulative density function of normal distribution
}
PutPayoff_tp1 <- function(S_tp0, S_tp1, X) {
pmax(0, (1-X) * S_tp0 - S_tp1)
}
Call_t <- function(S_tp0, Y, r_t, sigma_t) {
d1 <- (log(1/(1+Y)) + (r_t + sigma_t^2/2) * 1/12) / (sigma_t * sqrt(1/12))
d2 <- d1 - sigma_t * sqrt(1/12)
S_tp0 * pnorm(d1) - (1+Y) * S_tp0*exp(-r_t/12) * pnorm(d2)
}
CallPayout_tp1 <- function(S_tp0, S_tp1, Y) {
pmax(0, S_tp1 - (1+Y) * S_tp0)
}
…and finally the function for the actual return of the strike-conversion strategy, i.e. the core of the options strategy backtesting engine:
ROR_t <- function(S_tp0, S_tp1, X, Y, r_t, sigma_t) {
(S_tp1 + PutPayoff_tp1(S_tp0, S_tp1, X) - CallPayout_tp1(S_tp0, S_tp1, Y)) / (S_tp0 + Put_t(S_tp0, X, r_t, sigma_t) - Call_t(S_tp0, Y, r_t, sigma_t))
}
Putting it all together and letting the actual backtest run:
strategy_return <- ROR_t(S_tp0, S_tp1, X, Y, r_t, sigma_t) - 1
benchmark_return <- (S_tp1 / S_tp0) - 1
# create a data.frame with both data and with the dates (monthly basis)
months <- seq(as.Date("1990-11-1"), by = "month", length = length(S_tp0))
perf <- data.frame(months, strategy_return, benchmark_return)
colnames(perf) <- c("months", "Strike-Conversion Strategy", "S&P 100")
# create an xts out of the data frame
perfxts <- xts(perf[ , -1], order.by = perf[ , 1])
We can now calculate a multitude of performance and risk statistics:
table.Stats(perfxts) ## Strike-Conversion Strategy S&P 100 ## Observations 216.0000 216.0000 ## NAs 0.0000 0.0000 ## Minimum -0.0341 -0.1459 ## Quartile 1 -0.0107 -0.0181 ## Median 0.0174 0.0098 ## Arithmetic Mean 0.0083 0.0057 ## Geometric Mean 0.0080 0.0048 ## Quartile 3 0.0273 0.0320 ## Maximum 0.0338 0.1079 ## SE Mean 0.0015 0.0029 ## LCL Mean (0.95) 0.0053 0.0000 ## UCL Mean (0.95) 0.0112 0.0115 ## Variance 0.0005 0.0018 ## Stdev 0.0222 0.0426 ## Skewness -0.6451 -0.5578 ## Kurtosis -1.0751 1.0153 table.DownsideRisk(perfxts) ## Strike-Conversion Strategy S&P 100 ## Semi Deviation 0.0175 0.0321 ## Gain Deviation 0.0085 0.0244 ## Loss Deviation 0.0110 0.0314 ## Downside Deviation (MAR=10%) 0.0176 0.0334 ## Downside Deviation (Rf=0%) 0.0131 0.0293 ## Downside Deviation (0%) 0.0131 0.0293 ## Maximum Drawdown 0.1555 0.5078 ## Historical VaR (95%) -0.0311 -0.0724 ## Historical ES (95%) -0.0323 -0.0973 ## Modified VaR (95%) -0.0325 -0.0698 ## Modified ES (95%) -0.0347 -0.1005
Interestingly enough, the strike-conversion strategy yielded about the same mean return as the returns reported by Mr. Madoff… but with much bigger volatility (a.k.a. risk).
This was one of the tricks of Madoff to lull his investors into a sense of safety by not reporting over-the-top returns but “only” manipulating the price swings. His equity curve looked like being drawn with a ruler, which is of course totally unrealistic for an investment with this level of return.
A now for the big finale, the performance summary plot, which consists of the equity curves, the monthly returns, and the drawdowns…
charts.PerformanceSummary(perfxts)
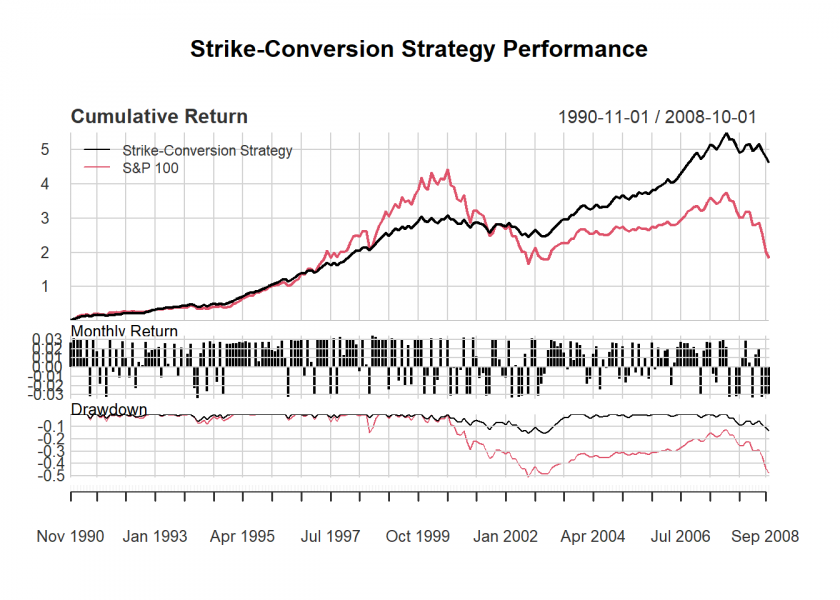
…the relative performance plot…
chart.RelativePerformance(perfxts[ , 1], perfxts[ , 2])
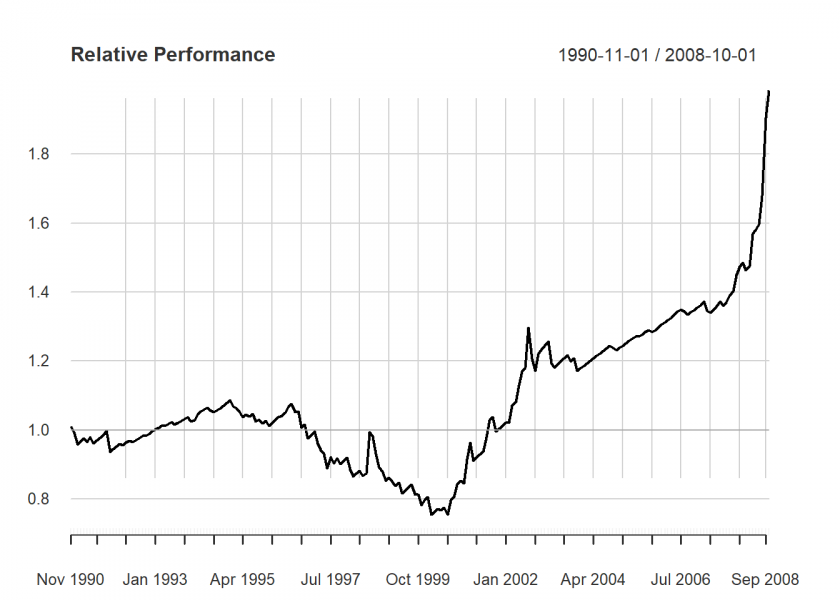
…and the risk-return scatterplot:
chart.RiskReturnScatter(perfxts)
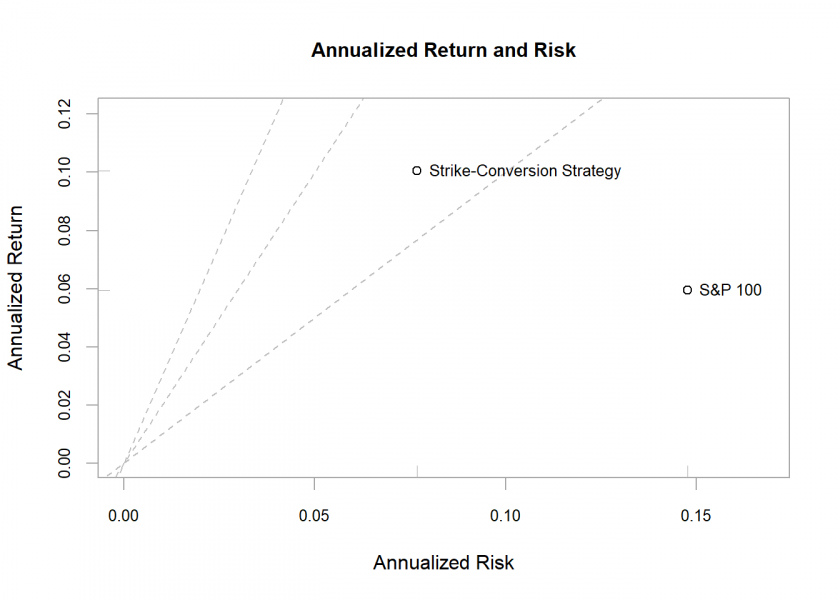
As you can see, the risk-return profile of the strike-conversion strategy is much better than that of the underlying index.
With this template you will now be able to backtest different options strategies of your own, you only have to modify ROR_t accordingly. I am looking forward to your insights and feedback in general in the comments.
BTW: I replicated another fascinating paper by Professor Stutzer: Parrondo’s Paradox in Finance: Combine two Losing Investments into a Winner.
DISCLAIMER
This post is written on an “as is” basis for educational purposes only and comes without any warranty. The findings and interpretations are exclusively those of the author and are not endorsed by or affiliated with any third party.
In particular, this post provides no investment advice! No responsibility is taken whatsoever if you lose money.
(If you make any money though I would be happy if you would buy me a coffee… that is not too much to ask, is it? 😉 )
UPDATE July 8, 2022
I created a non-technical video for this post (in German):

I read this paper a few years back. At the time thought it was a great opportunity to replicate in R. You beat me to the punch. Thanks for putting this together, and I hope to use this content in upcoming lessons.
Thank you, Mandip, for your great feedback, I really appreciate it! Feel free to use any material for teaching. If you have any ideas for improvements or clarification please let me know. Also, if you want to share any projects or lessons of your own as a guest post, please feel free to contact me.