
Modern movies use a lot of mathematics for their computer animations and CGI effects, one of them is what is known under the name fractals.
In this post, we will use this technique to create islands with coastlines that look extraordinarily realistic. If you want to do that yourself read on!
I was lucky enough to meet Professor Benoit Mandelbrot, one of the brightest minds of the past century and one of the fathers of fractal geometry, in person. One of his papers bears the title “How Long is the Coast of Britain?” where the so-called coastline paradox is being addressed: it basically states that the finer your ruler is the longer your overall result will be, so the coastline of a landmass does not have a well-defined length… an obviously counterintuitive result:
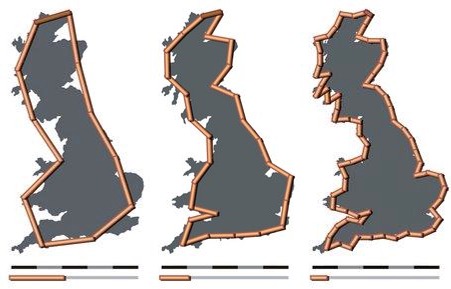
Here we will turn this principle on its head and use it to actually create realistic-looking landmasses with R. The inspiration for this came from chapter 4 “Infinite Detail” of the book “Math Bytes” by my colleague Professor T. Chartier from Davidson College in North Carolina.
The idea is to start with some very simple form, like a square, and add more detail step-by-step. Concretely, we go through every midpoint of our ever more complex polygon and shift it by a random amount. Because the polygon will be getting more and more intricate we have to adjust the absolute amount by which we shift the respective midpoints. That’s about all… have a look at the following code:
# define square
x <- c(0, 16, 16, 0, 0)
y <- c(0, 0, 16, 16, 0)
# function for generating random offsets of midpoints, change e.g. limit for your own experiments
realistic <- function(n, k) {
limit <- 0.5^k * 10
runif(n, -limit, limit)
}
# function for calculating all midpoints of a polygon
midpoints <- function(x) {
na.omit(filter(x, rep(1/2, 2)))
}
island <- function(x, y, iter = 10, random = realistic) {
# suppress "number of columns of result is not a multiple of vector length"-warnings because recycling is wanted here
oldw <- getOption("warn")
options(warn = -1)
for (i in 1:iter) {
# calculate midpoints of each line segment
x_m <- as.numeric(midpoints(x))
y_m <- as.numeric(midpoints(y))
# shift midpoint by random amount
x_m <- x_m + random(length(x_m), i)
y_m <- y_m + random(length(y_m), i)
#insert new midpoints into existing coordinates of polygon
x_n <- c(rbind(x, x_m))
x_n <- x_n[-length(x_n)]
y_n <- c(rbind(y, y_m))
y_n <- y_n[-length(y_n)]
x <- x_n
y <- y_n
}
options(warn = oldw)
list(x = x, y = y)
}
plot_island <- function(coord, island_col = "darkgreen", water_col = "lightblue") {
oldp <- par(bg = water_col)
plot(coord$x, coord$y, type = "n", axes = FALSE, frame.plot = FALSE, ann = FALSE)
polygon(coord$x, coord$y, col = island_col)
par(oldp)
}
Perhaps one thing is worth mentioning concerning the interaction of the functions: island receives the realistic function as an argument, which is a very elegant way of modularizing the code in case you want to try different randomizing functions. This extraordinary feature is possible because R is a functional programming language where functions are first-class citizens (for an introduction on this see here: Learning R: A gentle introduction to higher-order functions).
But now for some serious terra-forming:
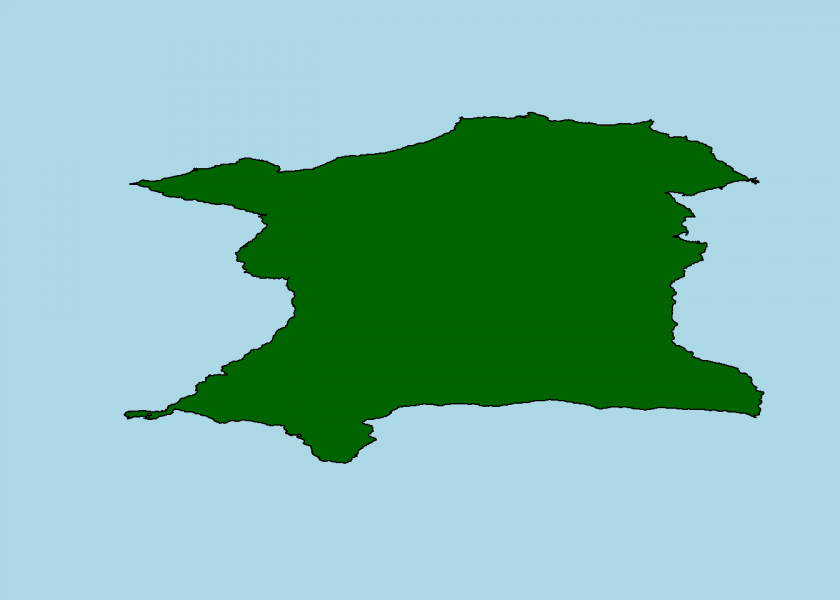
set.seed(1) # for reproducability coord <- island(x, y) plot_island(coord)
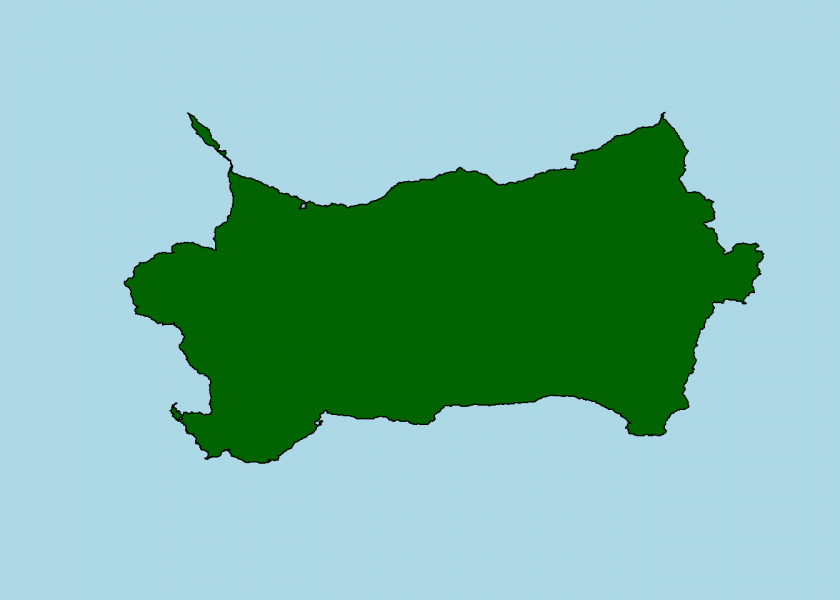
set.seed(3) coord <- island(x, y) plot_island(coord)
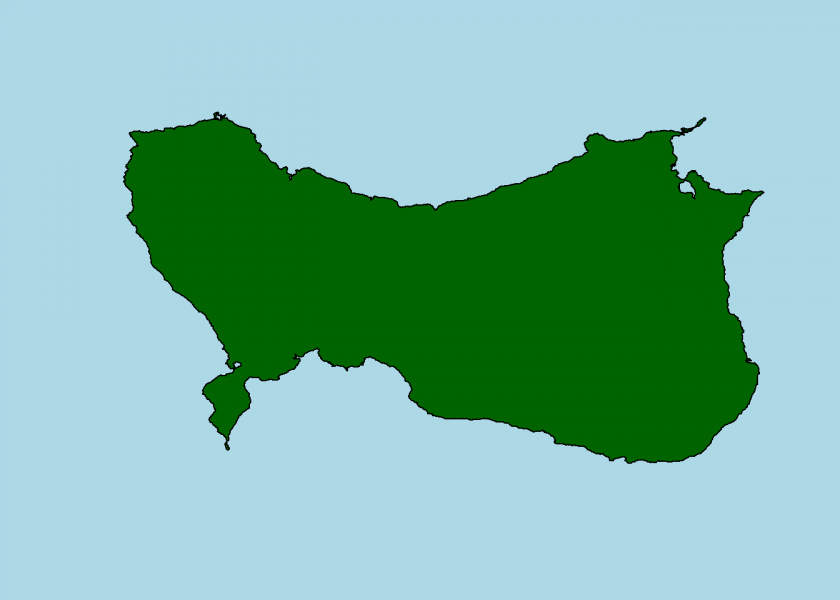
We can also observe the process step-by-step:
set.seed(2) coord <- island(x, y) plot_island(coord)
set.seed(2) coord <- island(x, y, iter = 1) plot_island(coord)

set.seed(2) coord <- island(x, y, iter = 2) plot_island(coord)

set.seed(2) coord <- island(x, y, iter = 4) plot_island(coord)
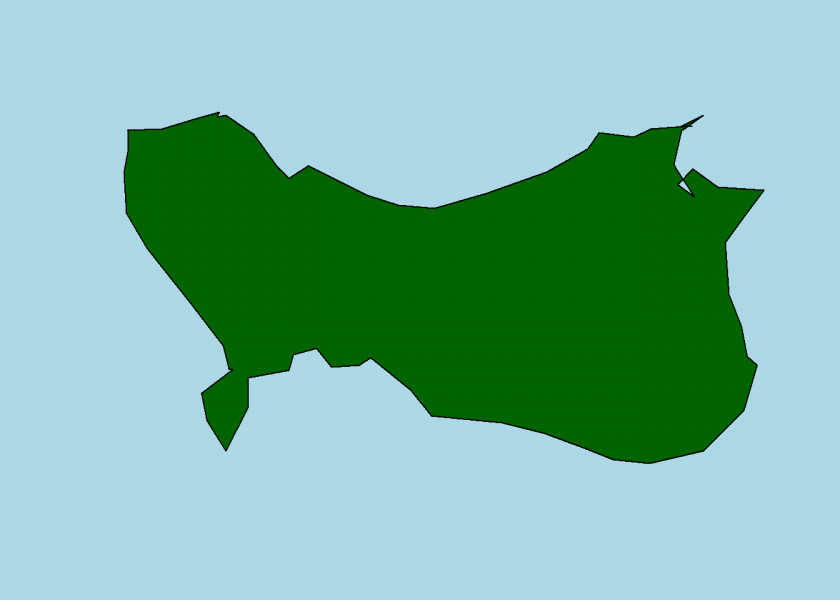
set.seed(2) coord <- island(x, y, iter = 6) plot_island(coord)
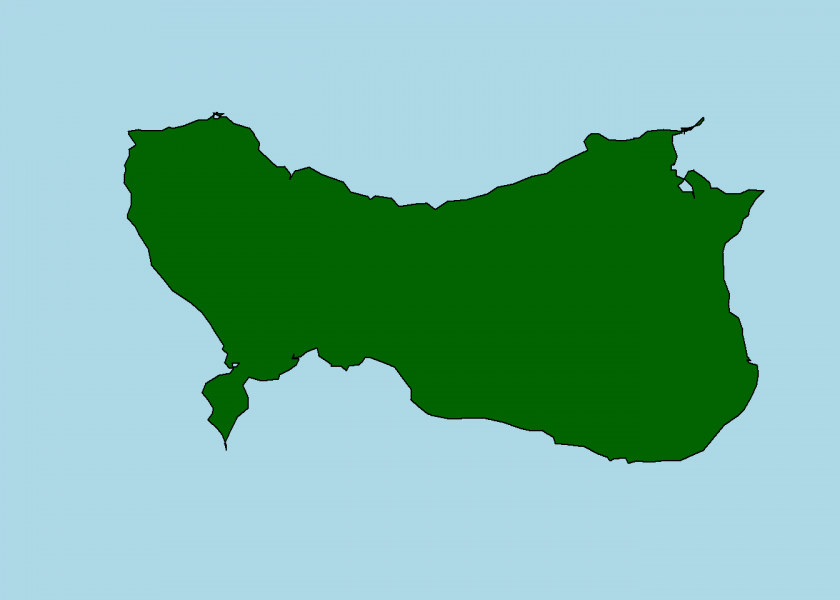
set.seed(2) coord <- island(x, y, iter = 8) plot_island(coord)
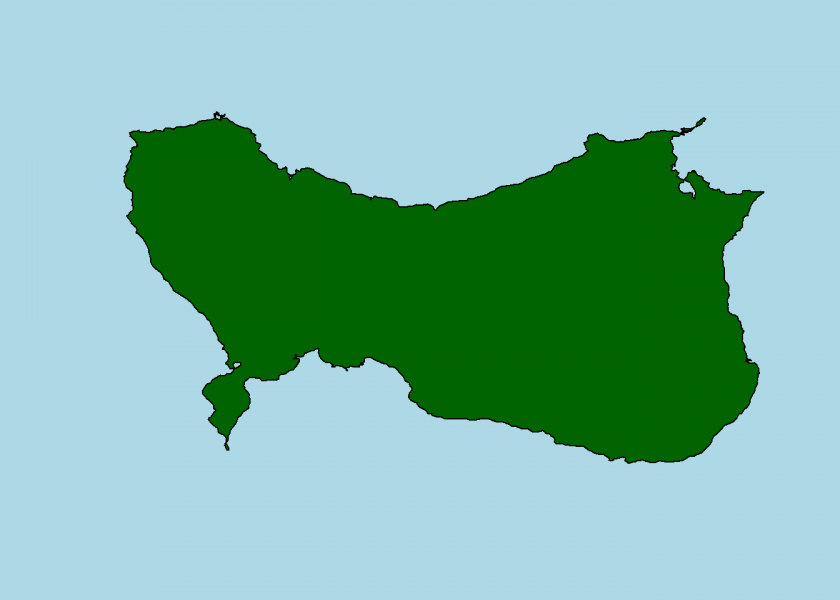
If you do your own experiments with the randomizer function and/or the seed and find an especially appealing example, please share it with us in the comments!
As a bonus, I would like to draw your attention to this little masterpiece of an educational film on fractals, created in the style of the great “Sin City” flick (~ 5 min.):
So, let me end this post with one last example of a volcanic island in a sea of lava… 😉
set.seed(5214) coord <- island(x, y) plot_island(coord, island_col = "black", water_col = "darkred")


Nice post! It is really similar to the post of Fernando Villalba Bergado in his blog (in Spanish) to generate ramdom islands and two more posts about the creation of treasure islands and how to identify whether a point is a cape or a gulf. You should have a look at them:
1. Generator of random islands (https://enrdados.netlify.com/post/generador-de-islas-aleatorias/)
2. Treasure islands (https://enrdados.netlify.com/post/mapa-del-tesoro/)
3. Algorithm forvcapes and gulfs (https://enrdados.netlify.com/post/algoritmo-golfo-cabo/)
Best regards
Very interesting, thank you! Didn’t know those (nor do I speak Spanish).
Well, at least the code is in R and the figures are language-agnostic!
Best regards
Reticulating splines.
“Reticulating splines (including many derivative forms) is a phrase included in many Maxis games (or their non-Maxis successors), including SimCity (SimCity 2000 and later), SimCopter, The Sims, The Sims 2, The Sims 3, and The Sims 4. The phrase is most often shown in text while on a load screen, though in its first appearance in SimCity 2000, it was spoken by a female voice. The term has become a somewhat well known in-joke and reference to SimCity or Maxis games in general.
The words ‘reticulate’ and ‘spline’ both have dictionary definitions, which has led several people to determine a meaning for the phrase, such as “to make a network of curved elements.” However, Will Wright stated in an interview that the term itself is meaningless, as SimCity 2000 does not reticulate splines when generating terrain; the phrase was included in the game because it “sounded cool.” It has since been included in many Maxis games, mostly for humor, much like the references to llamas in multiple games.”
Source: https://sims.fandom.com/wiki/Reticulating_splines
Next trick: use smoothed fractals to generate topological interiors for the island. Start with the island’s coastline, shrink slightly to create the first isocline, then apply some sort of random “shrinkage” to the perimeter points for the next isocline.
Sorry to be a pain, but: your midpoint randomizer leads to non-simple boundaries, i.e. when you connect the points the curve can cross over itself. This leads to “enclosed” lakes and violates true Fractal rules. I believe this is fixed by passing the entire set of x (or y) points to
realistic()to be used as the “maxlim” . To be exact, pass inmaxlim = c(x,x[1])to close the curve.This essentially changes the operation to become
> runif(length(x), 0.5^k*maxlim[-length(maxlim)], 0.5^k*maxlim[-1])That keeps the offsets from going out of range.
No, no, you are not a pain! I really appreciate your feedback! I will try it out later (at the moment I am rather busy…)
Could you please provide the whole function you adjust? At the moment it is unclear to me where to insert the changes exactly… Thank you!
This is really useful thanks. One note about the island function, you should use
stats::filterdplyr was taking ownership of “filter” of it without the specification. Sorry, I would likely dump tidy if I did not have to use other people’s code sometimes.
I would really like to see an exploration of Carl’s suggestion of a topological interior as I am trying to generate a mock lake with bathymetry. I will let you know if I come up with something.
Thank you for your feedback, highly appreciated!
Isn’t it sad that you now have to add R Base package namespaces to access standard R functions because they are overwritten by the tidyverse? For some general thoughts on the tidyverse: Why I don’t use the Tidyverse.
It would be great if you would extend the code, looking forward to hearing back from you!