
As we have already seen in former posts simple methods can be surprisingly successful in yielding good results (see e.g Learning Data Science: Predicting Income Brackets or Teach R to read handwritten Digits with just 4 Lines of Code).
If you want to learn how some simple mathematics, known as Naive Bayes, can help you find out the sentiment of texts (in this case movie reviews) read on!
The area we are dealing with here is called Natural Language Processing (NLP) and we already had some posts covering it (see Clustering the Bible and Extracting basic Plots from Novels: Dracula is a Man in a Hole).
We do this by using a simplified version of Bayes’ theorem (see Base Rate Fallacy – or why No One is justified to believe that Jesus rose). We will do it from scratch so that you really understand what is going on under the hood… but there are of course also excellent packages which will do it for you, most notably e1071 (on CRAN).
The big idea is to take texts that are already classified as “positive” and “negative” and use Bayes’ theorem to find the probability of words of unknown texts being positive/negative and sum over the probabilities for both categories to see which one “wins”.
Put differently, we find how probable positive/negative words are (basically by counting how frequently they appear in the given texts) and use that knowledge to weigh how positive or negative a new text is (by summing over all of the probabilities of both categories). Words that don’t signal a sentiment appear less often, relatively speaking (if the given texts are not systematically biased) or cancel each other out because they appear in both categories.
For the mathematical details, a quick repetitions of Bayes’ theorem (the vertical dash means “under the condition that”, P stands for probability):
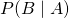 : appearance of the specific word (
: appearance of the specific word (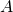 ) given the text is positive/negative (
) given the text is positive/negative (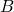 ) – this is what we know from our given texts.
) – this is what we know from our given texts.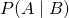 : the text is positive/negative (
: the text is positive/negative (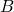 ) given the word appears (
) given the word appears (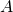 ) – this (whether the text is positive/negative) is what we want to know.
) – this (whether the text is positive/negative) is what we want to know.
To calculate one conditional probability from the other we use Bayes’ theorem:
![]()
Now, for some simplifications to make the calculations easier (and even possible!):
- The first simplification we make is that we eliminate the denominator with its
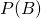 because it is the same for both probabilities: the appearance of the respective word is just the same for both expressions.
because it is the same for both probabilities: the appearance of the respective word is just the same for both expressions. - The second simplification also eliminates the
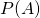 in the nominator because it will (at least in our example here) be more or less equal for both probabilities. Why? Because we will use the same amount of positive and negative example reviews (and by proxy about the same amount of positive and negative words).
in the nominator because it will (at least in our example here) be more or less equal for both probabilities. Why? Because we will use the same amount of positive and negative example reviews (and by proxy about the same amount of positive and negative words). - Now, we are coming to the “naive” part: we are not only talking about one word but about many words in the given texts. Obviously, their occurrence is not independent of each other, the probability that “good” is in the same text as “great” is higher than “good” being in the same text as “bad”. The problem is that our calculations would become super complicated (in the sense of impossible!) if we tried to model all of those dependencies: so we just assume that the occurrence of all words is independent of each other! Wow, that is a bold assumption… interestingly enough in practice, it works really great (as we are about to see…). So, we just multiply all of the probabilities of all of the words as if they were independent!
Two additional points:
- There will be cases where we find words in the new text that is not in the given texts. This would give
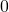 for the respective probability and because we multiply all of the probabilities the overall probability would give
for the respective probability and because we multiply all of the probabilities the overall probability would give 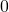 … not very helpful! Therefore we add
… not very helpful! Therefore we add 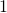 to all frequencies. This technique is called Laplace smoothing (or additive smoothing).
to all frequencies. This technique is called Laplace smoothing (or additive smoothing). - Because the probabilities for every given word is relatively small multiplying many of those small probabilities will give us even smaller probabilities and, in the end, is likely to give us an underflow error. Therefore we are going to use the
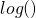 function on all probabilities and instead of multiplying all of them we sum them up (btw, we still have to add
function on all probabilities and instead of multiplying all of them we sum them up (btw, we still have to add 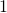 to the frequencies because
to the frequencies because 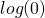 is undefined!).
is undefined!).
That was a lot of theory, let us now see the method work its magic in practice!
The original source of the data set is from here: Movie Review Data. It consists of 1,000 positive and 1,000 negative reviews. I created two files with all of the positive and negatives reviews respectively and zipped them so that they can be used directly for our purpose: Reviews.zip.
First unpack the archive and load the data into R:
pos <- readChar("data/pos.txt", file.info("data/pos.txt")$size)
neg <- readChar("data/neg.txt", file.info("data/neg.txt")$size)
Bag-of-words model: the following is a very simple function to tokenize the text, i.e. separate all the words, filter out relevant stuff and in this case only retain words that consist of more than 3 characters (so stop words such as “the”, “a”, “an”, “in” are not part of the analysis):
tokenize <- function(text) {
text <- tolower(text)
text <- gsub(". ", " ", text, fixed = TRUE)
text <- gsub(": ", " ", text, fixed = TRUE)
text <- gsub("? ", " ", text, fixed = TRUE)
text <- gsub("! ", " ", text, fixed = TRUE)
text <- gsub("; ", " ", text, fixed = TRUE)
text <- gsub(", ", " ", text, fixed = TRUE)
text <- gsub("\`", " ", text, fixed = TRUE)
text <- gsub("\n", " ", text, fixed = TRUE)
text <- unlist(strsplit(text, " "))
text[nchar(text) > 3]
}
pos_tokens <- tokenize(pos); neg_tokens <- tokenize(neg)
The following function calculates the log-probability of occurrence for a given token:
calc_Probs <- function(tokens) {
counts <- table(tokens) + 1
log(counts/sum(counts))
}
pos_probs <- calc_Probs(pos_tokens); neg_probs <- calc_Probs(neg_tokens)
As indicated in the text we also need a function to calculate the probability of occurrence for tokens that don’t happen to appear in the text:
calc_Prob_Rare <- function(tokens) {
counts <- table(tokens) + 1
log(1/sum(counts))
}
pos_probs_rare <- calc_Prob_Rare(pos_tokens); neg_probs_rare <- calc_Prob_Rare(neg_tokens)
Now, we are good to go! The next function calculates the positive and negative sentiment according to the process described above. Note that in the case that a word is not found in the given text the probability will be calculated taking pos_probs_rare or neg_probs_rare calculated before. Also, note that all probabilities are summed up because of the logarithm. At the end we just compare the two frequencies and return which is bigger:
calc_Sentiment <- function(review) {
test <- tokenize(review)
pos_pred <- sum(is.na(pos_probs[test])) * pos_probs_rare + sum(pos_probs[test], na.rm = TRUE)
neg_pred <- sum(is.na(neg_probs[test])) * neg_probs_rare + sum(neg_probs[test], na.rm = TRUE)
ifelse(pos_pred > neg_pred, "positive", "negative")
}
# positive
calc_Sentiment("This is a wonderful movie. I really loved it!")
## [1] "positive"
calc_Sentiment("I found this film so awesome, it made me cry")
## [1] "positive"
calc_Sentiment("I have never seen such a great movie. Best ever")
## [1] "positive"
# negative
calc_Sentiment("This is a horrible movie. I really hated it!")
## [1] "negative"
calc_Sentiment("I have never seen such crap. The director should be fired")
## [1] "negative"
calc_Sentiment("What should I say... This is the worst movie ever")
## [1] "negative"
This seems to work alright! Now, for the big finale… we are going to take two original reviews from the Internet Movie Database (IMDb), first a positive one after that a negative one:
# http://www.imdb.com/title/tt0111161/?pf_rd_m=A2FGELUUNOQJNL&pf_rd_p=2164853282&pf_rd_r=0GV6ZKG9Q9YXNSJM6QNT&pf_rd_s=center-1&pf_rd_t=15506&pf_rd_i=top&ref_=chttp_tt_1
# 10/10 -> positive
calc_Sentiment("Misery and Stand By Me were the best adaptations up until this one, now you can add Shawshank to that list. This is simply one of the best films ever made and I know I am not the first to say that and I certainly won't be the last. The standing on the IMDb is a true barometer of that. #3 as of this date and I'm sure it could be number 1. So I'll just skip all the normal praise of the film because we all know how great it is. But let me perhaps add that what I find so fascinating about Shawshank is that Stephen King wrote it. King is one of the best writers in the world. Books like IT and the Castle Rock series are some of the greatest stories ever told. But his best adaptations are always done by the best directors. The Shining was brilliantly interpreted by Kubrick and of course the aforementioned Misery and Stand By Me are both by Rob Reiner. Now Frank Darabont comes onto the scene and makes arguably the best King film ever. He seems to understand what King wants to say and he conveys that beautifully. What makes this film one of the best ever made is the message it conveys. It is one of eternal hope. Andy Dufresne, played by Tim Robbins, has been sent to prison for a crime he did not commit. But he never loses hope. He never gives up his quest to become a free man again. His years of tenacity, patience and wits keep him not only sane, but it gives his mind and a spirit a will to live. This film has a different feel to it. There has never been anything like it before and I don't know if there will again. I'm not going to say any more about this film, it has already been said, but just suffice to say that I am glad that Forrest Gump won best picture in 94. I would have been equally glad if Pulp Fiction or Shawshank would have won. It is that good of a movie and one that will be appreciated for years to come.")
## [1] "positive"
# http://www.imdb.com/title/tt2071491/?pf_rd_m=A2FGELUUNOQJNL&pf_rd_p=2164859782&pf_rd_r=1ZS06QED60VF2ZC2P2EV&pf_rd_s=center-1&pf_rd_t=15506&pf_rd_i=bottom&ref_=chtbtm_tt_2
# 1/10 -> negative
calc_Sentiment("Brett Kelly - super cheap director located in Canada with a huge potential to become 'worst director ever born' (nomination for 'Worst movie ever made' is also a must for pretty much every single feature he directs) did it again....I mean seriously? 'Jurassic Shark' (yeah I know it rather wasn't original title and was changed because from the marketing point of view it sounds 'hot') is one of the worst piece of garbage you will ever encounter. It makes Asylum movies look like a spectacular Hollywood blockbusters(but then again Asylum spends at least 50-100k for their movies). Kelly's modus operandi is 'we have a free 10k, let's shoot the movie') and it shows on the screen. Acting was never even remotely close to decent in his movies but with 'Jurassic Shark' it reaches the bottom(or something below bottom if it exists). Two blonde bimbos(not really attractive by any means) sitting in bikini on the beach for the first few minutes of the movie are asking to be bitch-slapped for doing what they are doing(which I don't know what is but not acting, that's for sure) and the director should be mutilated for casting them. As far as the special effects go, there aren't any, but if you are asking about 'horrible special effects wannabes' - yes sir, there are quite a few. From the piece of wood called 'shark' to cgi shark which looks so bad, that I don't even know what can I compare with it? (probably only sand castles build by mentally disabled 5 years old kids). I could go on and on(others did it as I see) but I really have no desire to write any longer about this piece of garbage. There is absolutely nothing good to be said about this movie and even though Brett Kelly did one watchable movie in the past 'Prey for the Beast' (and remember, I said 'watchable' not 'decent') I won't be fooled ever again and won't buy any of his movies again. Let them stay where they belong - in a trash bin.")
## [1] "negative"
Wow, the simple piece of algorithmic wonder classified both correctly!
As you can imagine the same technique can be used for spam filtering, or categorizing texts into different areas like politics, business, sports, etc.
Sometimes it just pays to be naive…

Thanks very much for an excellent article about naive Bayes, NLP and sentiment analysis!
Besides the article cited in this article, what other resources (classes, MOOCs, texts, articles, books) would the author recommend to learn more?
Thank you very much!
Sorry for answering so late, Stuart… and thank you very much for your great feedback, which is highly appreciated!
I had hoped that others would provide some pointers because, to be honest with you, I don’t have any in mind at the moment…
If you have found something worthwhile in the meantime please share it with us.
Thank you!
The tutorial is great.
But how can we apply the same for a big csv file.
to predict