Doing Maths Symbolically: R as a Computer Algebra System (CAS)

When I first saw the Computer Algebra System Mathematica in the nineties I was instantly fascinated by it: you could not just calculate things with it but solve equations, simplify, differentiate and integrate expressions and even solve simple differential equations… not just numerically but symbolically! It helped me a lot during my studies at the university back then. Normally you cannot do this kind of stuff with R but fear not, there is, of course, a package for that!

There are many so-called Computer Algebra Systems (CAS) out there, commercial but also open-source. One very mature one is called YACAS (for Yet Another Computer Algebra System). You find the documentation here: Yacas Documentation (many of the following examples are taken from there).

You can use the full power of it in R by installing the Ryacas package from CRAN. You can use Yacas commands directly by invoking the yac_str function, the as_r function converts the output to R. Let us first simplify a mathematical expression:

library(Ryacas)
## 
## Attaching package: 'Ryacas'
## The following object is masked from 'package:stats':
## 
##     deriv
## The following objects are masked from 'package:base':
## 
##     %*%, determinant, diag, diag<-, I, lower.tri, upper.tri

# simplify expressions
as_r(yac_str("Simplify(a*b*a^2/b-a^3)"))
## [1] 0

Or solve an equation:

as_r(yac_str("Solve(a+x*y==z,x)"))
## [1] "x==-(a-z)/y"

And you can do all kinds of tedious stuff that is quite error-prone when done differently, e.g. expanding expressions like by using the binomial theorem:

as_r(yac_str("Expand((x-2)^20)"))
## expression(x^20 - 40 * x^19 + 760 * x^18 - 9120 * x^17 + 77520 * 
##     x^16 - 496128 * x^15 + 2480640 * x^14 - 9922560 * x^13 + 
##     32248320 * x^12 - 85995520 * x^11 + 189190144 * x^10 - 343982080 * 
##     x^9 + 515973120 * x^8 - 635043840 * x^7 + 635043840 * x^6 - 
##     508035072 * x^5 + 317521920 * x^4 - 149422080 * x^3 + 49807360 * 
##     x^2 - 10485760 * x + 1048576)

To demonstrate how easily the results can be integrated into R let us do some curve sketching on a function. First, we define two helper function for converting an expression into a function (which can then be used to plot it) and for determining the derivative of order n of some function (we redefine the D function for that):

as_function <- function(expr) {
  as.function(alist(x =, eval(parse(text = expr))))
}

# redefine D function
D <- function(eq, order = 1) {
  yac_str(paste("D(x,", order, ")", eq))
}

Now, we define the function (in this case a simple polynomial ), determine the first and second derivatives symbolically and plot everything:

xmin <- -5
xmax <- 5

eq <- "2*x^3 - 3*x^2 + 4*x - 5"
eq_f <- as_function(eq)
curve(eq_f, xmin, xmax, ylab = "y(x)")
abline(h = 0, lty = 2)
abline(v = 0, lty = 2)

D_eq <- D(eq)
D_eq
## [1] "6*x^2-6*x+4"

D_eq_f <- as_function(D_eq)
curve(D_eq_f, xmin, xmax, add = TRUE, col = "blue")

D2_eq <- D(eq, 2)
D2_eq
## [1] "12*x-6"

D2_eq_f <- as_function(D2_eq)
curve(D2_eq_f, xmin, xmax, add = TRUE, col = "green")

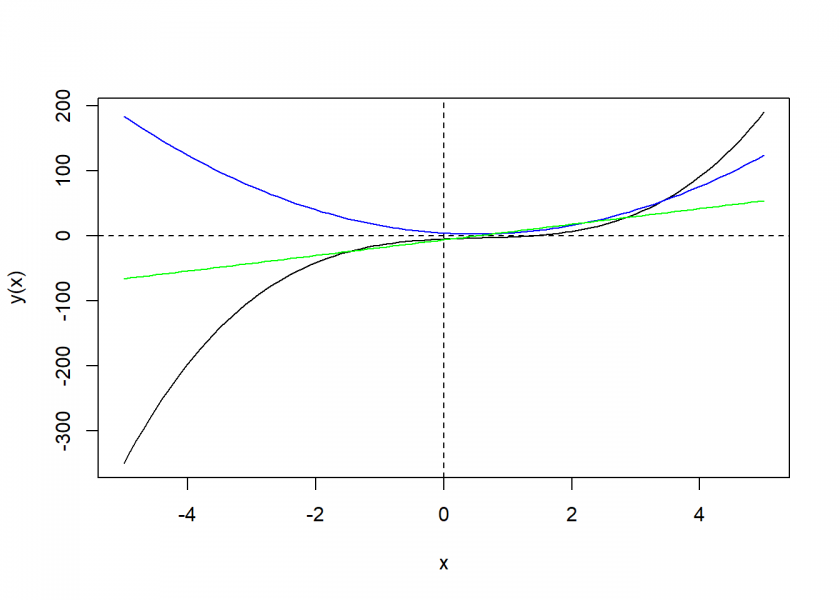
Impressive, isn’t it! Yacas can also determine limits and integrals:

# determine limits
yac_str("Limit(x,0) 1/x")
## [1] "Undefined"

yac_str("Limit(x,0,Left) 1/x")
## [1] "-Infinity"

yac_str("Limit(x,0,Right) 1/x")
## [1] "Infinity"

# integration
yac_str("Integrate(x) Cos(x)")
## [1] "Sin(x)"

yac_str("Integrate(x,a,b) Cos(x)")
## [1] "Sin(b)-Sin(a)"

As an example, we can prove in no-time that the famous approximation is actually too big (more details can be found here: Proof that 22/7 exceeds π):

   

yac_str("Integrate(x,0,1) x^4*(1-x)^4/(1+x^2)")
## [1] "22/7-Pi"

And, as the grand finale of this post, Yacas is even able to solve ordinary differential equations symbolically! Let us first take the simplest of them all:

as_r(yac_str("OdeSolve(y' == y)"))
## expression(C115 * exp(x))

It correctly returns the exponential function (The C-term is just an arbitrary constant). And finally a more complex, higher-order one:

as_r(yac_str("OdeSolve(y'' - 4*y == 0)"))
## expression(C154 * exp(2 * x) + C158 * exp(-2 * x))

I still find CAS amazing and extremely useful… and an especially powerful one can be used from within R!