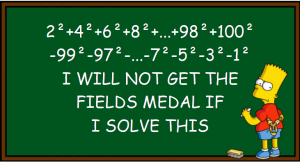R Coding Challenge: 7 (+1) Ways to Solve a Simple Puzzle

This time we want to solve the following simple task with R: Take the numbers 1 to 100, square them, and add all the even numbers while subtracting the odd ones!

If you want to see how to do that in at least seven different ways in R, read on!

There are many different solutions possible, making use of several aspects of the R language. So this blog post can be seen as a fun exercise to recap some of the concepts explained in our introduction to R: Learning R: The Ultimate Introduction (incl. Machine Learning!).

First, as usual, you should try this for yourself…

Ok, so if you didn’t have any ideas whatsoever you could have done it by hand, i.e. use R as a calculator:

2^2 + 4^2 + 6^2 + 8^2 + 10^2 + 12^2 + 14^2 + 16^2 + 18^2 + 20^2 + 22^2 + 24^2 + 26^2 + 28^2 + 30^2 + 32^2 + 34^2 + 36^2 + 38^2 + 40^2 + 42^2 + 44^2 + 46^2 + 48^2 + 50^2 + 52^2 + 54^2 + 56^2 + 58^2 + 60^2 + 62^2 + 64^2 + 66^2 + 68^2 + 70^2 + 72^2 + 74^2 + 76^2 + 78^2 + 80^2 + 82^2 + 84^2 + 86^2 + 88^2 + 90^2 + 92^2 + 94^2 + 96^2 + 98^2 + 100^2
- 99^2 - 97^2 - 95^2 - 93^2 - 91^2 - 89^2 - 87^2 - 85^2 - 83^2 - 81^2 - 79^2 - 77^2 - 75^2 - 73^2 - 71^2 - 69^2 - 67^2 - 65^2 - 63^2 - 61^2 - 59^2 - 57^2 - 55^2 - 53^2 - 51^2 - 49^2 - 47^2 - 45^2 - 43^2 - 41^2 - 39^2 - 37^2 - 35^2 - 33^2 - 31^2 - 29^2 - 27^2 - 25^2 - 23^2 - 21^2 - 19^2 - 17^2 - 15^2 - 13^2 - 11^2 - 9^2 - 7^2 - 5^2 - 3^2 - 1^2
## [1] 5050

The result is 5050. But there are of course many much more elegant solutions. The first solution I thought of was the following, it makes use of the seq function:

sum(seq(2, 100, 2)^2 - seq(99, 1, -2)^2)
## [1] 5050

An integral part is splitting the numbers into 50 even and 50 odd ones. There are several ways to do that. One way is to create both with the formulas 2n for even and 2n-1 for odd numbers:

n <- 1:50
even <- 2 * n
odd <- 2 * n - 1
sum(even^2 - odd^2)
## [1] 5050

Another possibility is by subsetting with recycling…

x <- 1:100
even <- x[c(FALSE, TRUE)] # subsetting with recycling
odd <- x[c(TRUE, FALSE)]
sum(even^2 - odd^2)
## [1] 5050

…or elegantly by creating a matrix:

M <- matrix(1:100, nrow = 2)
sum(M[2, ]^2 - M[1, ]^2)
## [1] 5050

If you come from another language, especially C and its derivatives you might have wanted to use a loop. This is of course also possible but discouraged in R (some say that you then “speak R with a C accent”):

s <- 0
for (x in 1:100) {
  if (x %% 2) s <- s - x^2
  else s <- s + x^2
}
s
## [1] 5050

As you can see, inside of the for loop is a conditional statement and the modulo operator (%%) to get the remainder of a division. It might seem a little counterintuitive that x %% 2 gives FALSE when x is even (= no remainder) and TRUE when it is odd. The reason for this is that when there is no remainder (= even), this evaluates to FALSE because 0 is the internal representation for FALSE, while 1 is the internal representation for TRUE (remainder of 1 -> odd).

The following version might be a little clearer in this respect while being slightly longer (the statements after if and else are now switched):

s <- 0
for (x in 1:100) {
  if (x %% 2 == 0) s <- s + x^2
  else s <- s - x^2
}
s
## [1] 5050

The original loop can easily be vectorized which is the preferred method in R:

x <- 1:100
sum(ifelse(x %% 2, -x^2, x^2)) # vectorized if statement
## [1] 5050

Those were seven ways to get to the same correct result… and now for the bonus: if you think long enough about this little riddle you will see that is equivalent to adding up the original numbers (I leave this as an exercise, it is not too hard to see). The resulting code out of this analysis couldn’t be any simpler:

sum(1:100) # analytical
## [1] 5050

That was fun, wasn’t it! If you want to share your own solution, please do so in the comments below. If it is an especially clever, elegant, or creative one you will get an honorary mention in an update of this post!

P.S.: The Bart Simpson blackboard pic was created with the code provided in this post: Create Bart Simpson Blackboard Memes with R.

---

UPDATE June 24, 2021
A very concise and elegant solution came from Rob in the comments:

sum(c(-1, 1) * (1:100)^2)
## [1] 5050

---

UPDATE July 28, 2021
The most elegant and concise solution came from NelaTo in the comments – well done!

x <- 1:100
sum((-1)^x * x^2)
## [1] 5050

---

UPDATE May 2, 2023
I asked ChatGPT to come up with the following versions: while loop, repeat loop, and a recursive version. It got all three right, although I simplified its code a little:

s <- 0
x <- 1
while (x <= 100) {
  if (x %% 2) s <- s - x^2
  else s <- s + x^2
  x <- x + 1
}
s
## [1] 5050

s <- 0
x <- 1
repeat {
  if (x %% 2) s <- s - x^2
  else s <- s + x^2
  x <- x + 1
  if (x > 100) break
}
s
## [1] 5050

calculate_s <- function(x, s) {
  if (x > 100) return(s)
  if (x %% 2) s <- s - x^2
  else s <- s + x^2
  calculate_s(x + 1, s)
}
calculate_s(1, 0)
## [1] 5050