
Over one billion dollars have been spent in the US to split up big schools into smaller ones because small schools regularly show up in rankings as top performers.
In this post, I will show you why that money was wasted because of a widespread (but not so well known) statistical artifact, so read on!
Why do small schools perform better? Many are quick to point out that an intimate, family-like atmosphere helps facilitate learning and smaller units can cater more to the special needs of their pupils. But is this really the case?
Let us conduct a little experiment where we distribute randomly performing pupils on one thousand schools, where half of them are big and the other half small. To be clear: we distribute those pupils by chance alone so that every school should have the same shot at getting top, average-, and low performers!
As a proxy for performance let us just take the intelligence quotient (IQ) which is defined to be normally distributed with a mean of 100 and a standard deviation of 15.
Let us now have a look at the fifty best performing schools:
n <- 1000 # no of schools sm <- 50 # no of pupils small school bg <- 1000 # no of pupils big school set.seed(12345) small <- matrix(rnorm(n/2 * sm, mean = 100, sd = 15), nrow = n/2, ncol = sm) big <- matrix(rnorm(n/2 * bg, mean = 100, sd = 15), nrow = n/2, ncol = bg) df_small <- data.frame(size = "small", performance = rowMeans(small)) df_big <- data.frame(size = "big", performance = rowMeans(big)) df <- rbind(df_small, df_big) df_order <- df[order(df$performance, decreasing = TRUE), ] df_order |> head(50) ## size performance ## 296 small 106.3838 ## 464 small 105.9089 ## 128 small 105.5734 ## 146 small 105.2287 ## 36 small 104.9394 ## 479 small 104.7963 ## 406 small 104.7407 ## 126 small 104.7316 ## 386 small 104.6500 ## 15 small 104.6092 ## 183 small 104.5761 ## 492 small 104.5029 ## 106 small 104.5003 ## 330 small 104.3905 ## 456 small 104.2457 ## 84 small 104.2373 ## 474 small 104.1203 ## 89 small 103.9073 ## 315 small 103.7264 ## 108 small 103.5928 ## 19 small 103.5878 ## 268 small 103.5433 ## 435 small 103.4099 ## 481 small 103.2921 ## 70 small 103.2447 ## 110 small 103.2089 ## 96 small 103.1939 ## 497 small 103.1700 ## 103 small 103.1609 ## 262 small 103.1533 ## 33 small 103.1376 ## 293 small 103.1008 ## 252 small 103.0873 ## 240 small 103.0657 ## 170 small 103.0553 ## 220 small 103.0485 ## 185 small 103.0196 ## 195 small 103.0042 ## 98 small 102.9625 ## 294 small 102.9349 ## 51 small 102.9339 ## 317 small 102.9308 ## 403 small 102.9258 ## 202 small 102.9255 ## 463 small 102.9072 ## 321 small 102.8631 ## 124 small 102.8468 ## 380 small 102.8341 ## 273 small 102.8147 ## 217 small 102.8005
In fact, all of them are small! How is that possible?
You are in for another surprise when you also look at the fifty worst performers:
df_order |> tail(50) ## size performance ## 221 small 97.43354 ## 271 small 97.43122 ## 420 small 97.42636 ## 77 small 97.40313 ## 141 small 97.38554 ## 192 small 97.38214 ## 45 small 97.36123 ## 331 small 97.35636 ## 133 small 97.15977 ## 400 small 97.12790 ## 350 small 97.09748 ## 161 small 96.97677 ## 395 small 96.97156 ## 17 small 96.95732 ## 50 small 96.94013 ## 353 small 96.77378 ## 376 small 96.63066 ## 140 small 96.60068 ## 80 small 96.59475 ## 115 small 96.56996 ## 362 small 96.52821 ## 16 small 96.35869 ## 344 small 96.29919 ## 290 small 96.23309 ## 41 small 96.21083 ## 246 small 96.13112 ## 345 small 96.06559 ## 104 small 96.03273 ## 425 small 96.02648 ## 32 small 96.01366 ## 7 small 95.99434 ## 364 small 95.99399 ## 397 small 95.95282 ## 374 small 95.92229 ## 18 small 95.80126 ## 184 small 95.73809 ## 127 small 95.65754 ## 270 small 95.60595 ## 356 small 95.39492 ## 433 small 95.33532 ## 475 small 95.30683 ## 66 small 95.30076 ## 445 small 94.94566 ## 61 small 94.88395 ## 500 small 94.85970 ## 442 small 94.85128 ## 6 small 94.56465 ## 347 small 94.43273 ## 261 small 94.23249 ## 171 small 93.82268
Again, all of them are small! The following plot reveals the overall pattern:
(df_order$performance - 100) |> barplot(main = "Sorted relative performance of schools", col = ifelse(df_order$size == "small", "blue", "red"), border = NA)
abline(h = 0)
legend("bottomleft", legend = c("Small schools", "Big schools"), fill = c("blue", "red"), bty = "n")
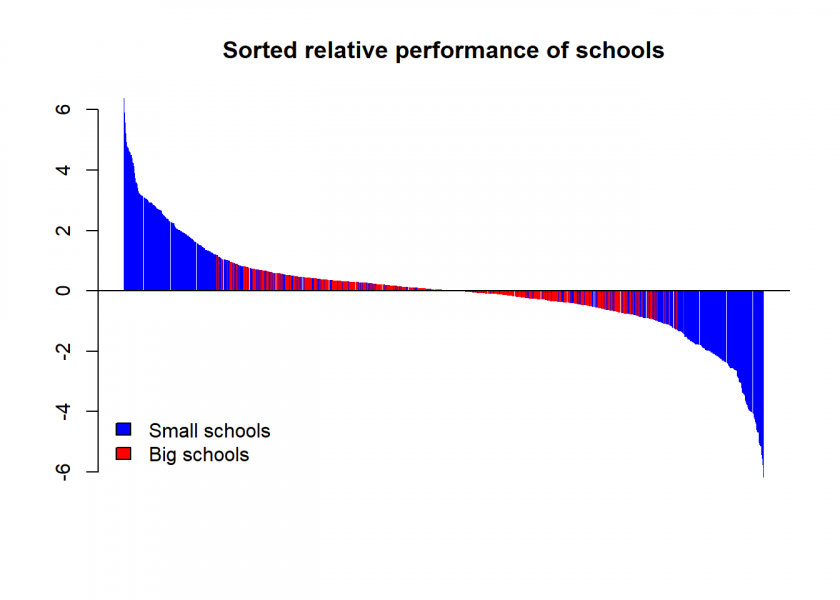
The statistical effect at work here is what my colleague Professor Howard Wainer from the University of Pennsylvania coined “The Most Dangerous Equation” in an article in the renowned American Scientist.
To understand this let us first look at some statistical measures:
summary(df_small$performance) ## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 93.82 98.59 100.06 100.01 101.42 106.38 summary(df_big$performance) ## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 98.58 99.71 100.02 99.99 100.32 101.19
We can see that, while both have the same mean performance, the performance variation is bigger for small schools than for big ones where the extreme cases are averaged out. De Moivre’s equation gives the exact relation in connection to the sample size, i.e. the number of pupils in this case:
![]()
where ![]() is the standard error of the mean,
is the standard error of the mean, ![]() is the standard deviation of the sample and
is the standard deviation of the sample and ![]() is the size of the sample.
is the size of the sample.
Let us calculate those numbers for our little example and compare them to the actual standard deviations of the school performance:
sd(df_small$performance) ## [1] 2.144287 15 / sqrt(sm) ## [1] 2.12132 sd(df_big$performance) ## [1] 0.4677121 15 / sqrt(bg) ## [1] 0.4743416
We can see that those numbers fit very well.
Basically, de Moivre’s equation tells us that the smaller the sample size (= the number of pupils per school) the bigger the variation (= standard error/standard deviation) which results in the effect that small schools inhabit both extremes of the performance rankings. When you only look at the top performers you will falsely conclude that you have to split up big schools!
In fact, later studies (which took this effect into account) even found that larger schools are better performing after all because they are able to offer a wider range of classes with teachers who can focus on fewer subjects. The “de Moivre”-effect was hiding this and turned it on its head!
Other examples of this widespread effect include:
- Disease rates in small and big cities, e.g. for cancer or COVID-19 infections. Small cities simultaneously lead and lag statistics compared to large cities. Sometimes even one single case can make all the difference.
- Traffic safety rates: same here, small cities are at each end of the spectrum.
- Quality of hospitals: regularly small houses end up being at the top and at the bottom.
- Mutual fund performance: there are often large swings in the performance of small funds which lets them show up in rankings on both extremes.
- …and the list goes on and on.
Of course, commentators are always fast to find reasons for each extreme, e.g. in the case of cancer rates: either “clean living of the rural lifestyle — no air pollution, no water pollution, access to fresh food without additives”, and so on vs. “poverty of the rural lifestyle — no access to good medical care, a high-fat diet, and too much alcohol and tobacco”, where in fact both results are mainly due to the statistical artifact explained by de Moivre’s equation!
This equation is so dangerous exactly because people don’t know it yet its effects are so far-reaching.
Another example of what can be called “Only looking at the winners-fallacy” can be found here: How to be Successful! The Role of Risk-taking: A Simulation Study. For another interesting fallacy due to sampling see: Collider Bias, or Are Hot Babes Dim and Eggheads Ugly?.
Do you have other examples where the “de Moivre”-effect creeps up? Please share your thoughts in the comments.
UPDATE January 5, 2023
I created a video for this post (in German):

Thanks for illustrating this effect so nicely and effectively!
Your simulation might be a good exercise for students of statistics. I recently came across a paper by Yanai and Lercher (2020) where they hid a gorilla in a data set that they asked students to analyse. If they made a simple scatter plot they would have found it, but many didn’t. The researchers found that students who were not given a specific hypothesis to test would explore the data more, and thus find the gorilla. Similarly, I imagine that people might stop exploring the IQ x school size data when they found that the best performing schools were small schools, and not notice what you show here, that they are also the worst schools.
Yanai, I., & Lercher, M. (2020). A hypothesis is a liability. Genome Biology, 21(1), Article 1. https://doi.org/10.1186/s13059-020-02133-w
Very interesting, thank you Håvard!
I the paper on my reading list. You might be interested in the following post: Causation doesn’t imply Correlation either (with the infamous datasaurus). It is quite an ingenious idea to let students find it, I think I will try this 😉
Wait — is the fallacy here the statistics or that the reviewing agencies are just looking at the TOP performing schools and comparing their size (I don’t know the answer). Because if the reviewing agencies simply looked at averages across small/large school groups, they would seem to balance out, because small schools are at both ends of the spectrum, right? If so, this would not really be a statistical issue but one of interpretation.
School classes typically consist of 25 pupils, so in a random class you have an even bigger spread than in the small school example, but if you’d compare classes in big and small schools they should be identical except for comfort factors such as the ones mentioned (“atmosphere helps facilitate learning and smaller units can cater more to the special needs of their pupils”)–I guess what I try to say is that focusing on means over larger and smaller samples is simply comparing apples and oranges.
Once again a very interesting analysis through simulation. Thanks for highlighting that. Having this in mind what do or other readers think to do to analyze the effect of class size on school performance?
Perfect would be something like an experiment, putting randomly pupils into classes of different size. Thereby checking for balanced school performance in classes and controlling for “all” other things that should have an effect on school performance (through a suitable test) (how and what to teach, teacher, school, IQ endowments of pupils, effort of parents, etc.) and then checking after a year how school performance evolved for different size classes.