
Tomorrow, on the First of May, many countries celebrate the so called International Workers’ Day (or Labour Day): time to talk about the unequal distribution of wealth again, so read on!
A few months ago I posted a piece with the title “If wealth had anything to do with intelligence…” where I argued that ability, e.g. intelligence, as an input has nothing to do with wealth as an output. It drew a lot of criticism (as expected), most of it unfounded in my opinion but one piece merits some discussion: the fact that the intelligence quotient (IQ) is normally distributed by construction. The argument goes that intelligence per se may be a distribution with fat tails too but by the way, the IQ is constructed the metric is being transformed into a well-formed gaussian distribution. To a degree, this is certainly true, yet I would still argue that the distribution of intelligence and all other human abilities are far more well behaved than the extremely unequal distribution of wealth. I wrote in a comment:
There are many aspects in your comment that are certainly true. Obviously, there are huge problems in measuring “true” mental abilities, which is the exact reason why people came up with a somewhat artificial “intelligence quotient” with all its shortcomings.
What would be interesting to see is (and I don’t know if you perhaps have a source about this) what the outcome of an intelligence test would look like without the “quotient” part, i.e. without subsequently normalizing the results.
I guess the relationship wouldn’t be strictly linear but it wouldn’t be as extreme as the wealth distribution either.
What I think is true in any case, independent of the distributions, is when you rank all people by intelligence and by wealth respectively you wouldn’t really see any stable connection – and that spirit was the intention of my post in the first place and I still stand by it, although some of the technicalities are obviously debatable.
So, if you have a source, Dear Reader, you are more than welcome to share it in the comments – I am always eager to learn!
I ended my post with:
But if it is not ability/intelligence that determines the distribution of wealth what else could account for the extreme inequality we perceive in the world?
In this post I will argue that luck is a good candidate!

In 2014 there was a special issue of the renowned magazine Science titled “The science of inequality”. In one of the articles (Cho, A.: “Physicists say it’s simple”) the following thought experiment is being proposed:
Suppose you randomly divide 500 million in income among 10,000 people. There’s only one way to give everyone an equal, 50,000 share. So if you’re doling out earnings randomly, equality is extremely unlikely. But there are countless ways to give a few people a lot of cash and many people a little or nothing. In fact, given all the ways you could divvy out income, most of them produce an exponential distribution of income.
So, the basic idea is to randomly throw 9,999 darts at a scale ranging from zero to 500 million and study the resulting distribution of intervals:
library(MASS) w <- 5e8 # wealth p <- 1e4 # no. of people set.seed(123) d <- diff(c(0, sort(runif(p-1, max = w)), w)) # wealth distribution h <- hist(d, col = "red", main = "Exponential decline", freq = FALSE, breaks = 45, xlim = c(0, quantile(d, 0.99))) fit <- fitdistr(d, "exponential") curve(dexp(x, rate = fit$estimate), col = "black", type = "p", pch = 16, add = TRUE)
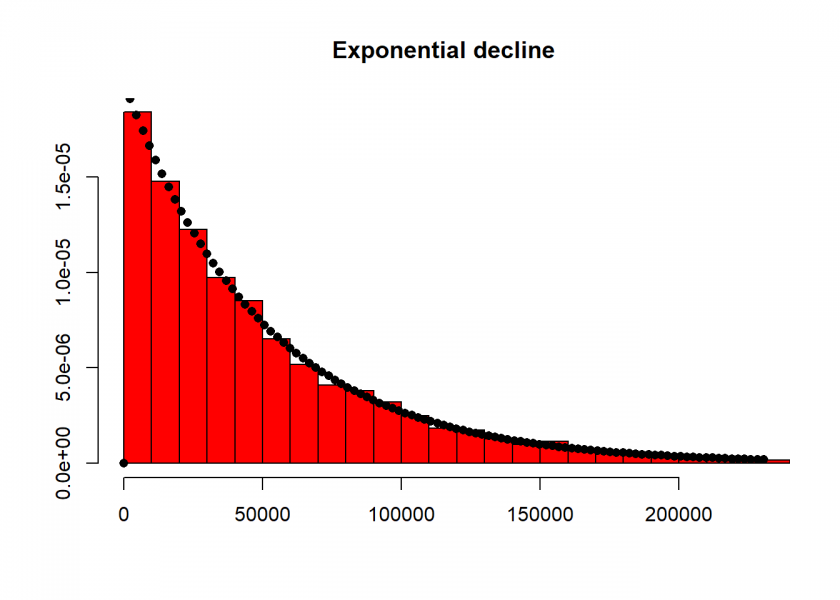
The resulting distribution fits an exponential distribution very well. You can read some interesting discussions concerning this result on CrossValidated StackExchange: How can I analytically prove that randomly dividing an amount results in an exponential distribution (of e.g. income and wealth)?
Just to give you an idea of how unfair this distribution is: the richest six persons have more wealth than the poorest ten percent together:
sum(sort(d)[9994:10000]) - sum(sort(d)[0:1000]) ## [1] 183670.8
If you think that this is ridiculous just look at the real global wealth distribution: here it is not six but three persons who own more than the poorest ten percent!
Now, what does that mean? Well, equality seems to be the exception and (extreme) inequality the rule. The intervals were found randomly, no interval had any special skills, just luck – and the result is (extreme) inequality – as in the real world!
If you can reproduce the wealth distribution of a society stochastically this could have the implication that it wasn’t so much the extraordinary skills of the rich which made them rich but they just got lucky.
Some rich people are decent enough to admit this. In his impressive essay “Why Poverty Is Like a Disease” Christian H. Cooper, a hillbilly turned investment banker writes:
So how did I get out? By chance.
It’s easy to attach a post-facto narrative of talent and hard work to my story because that’s what we’re fed by everything from Hollywood to political stump speeches. But it’s the wrong story. My escape was made up of a series of incredibly unlikely events, none of which I had real control over.
[…]
I am the exception that proves the rule—but that rule is that escape from poverty is a matter of chance and not a matter of merit.
A consequence would be that you cannot really learn much from the rich. So throw away all of your self-help books on how to become successful. I will end with a cartoon, which brings home this message, on a closely related concept, the so-called survivorship bias (which is also important to keep in mind when backtesting trading strategies in quantitative finance, the topic of an upcoming post… so stay tuned!):

UPDATE May 7, 2020
The post on backtesting trading strategies in quantitative finance is now online: Backtest Trading Strategies like a real Quant

I think that while it’s interesting that a purely luck based distribution results in an exponential distribution, it’s not necessarily the only way such a distribution could arise.
For example, let’s consider a reduced case. It’s well known that incomes of (for example) musicians and writers follow a highly skewed distribution. Of course, it would be very wrong to say that luck plays no role in success for these professions.
However, it would be equally wrong to say that skill and talent of a musician has no impact on their earnings. As a terrible musician, my odds of earning a high income from music are very low indeed. A very talented musician may still not have great chances of earning high income, but their chances are much higher than mine.
Well, to be honest with you I think you gave the perfect example for an industry that is mainly driven by luck!
There are millions of talented writers and musicians out there but only a few rake in millions of dollars, euros, pounds while most of them don’t know how to pay their rent this month. Do you really think that the people in the bestseller lists and in the charts are millions of times more talented than their not so successful colleagues…?!? I personally doubt it.
On point … regarding the distribution of talent IMHO similar reasoning goes for sports in the sense that if you stay in the domain (eg all soccer players) there has to be a huge amount of luck involved to rank in the multi-million dollar contract (and of course no injuries)
Awesome post by the way … looking forward to your next one
Good point, Walter! And thank you for your great feedback, I really appreciate it.
Adding to my comment above: I just found this interesting piece about JK Rowling by Duncan J. Watts:
https://gulfnews.com/opinion/op-eds/jk-rowling-fame-by-chance-or-true-genius-1.1213337
You should read the full article (because there is a lot of scientific background information) but the following paragraph about her publishing under a pseudonym will give you some idea:
“Rowling made a bold move […]: Until the news leaked about the author’s real identity, this critically acclaimed book had sold only 500 to 1,500 copies, depending on which report you read. What is more, had the author actually been Robert Galbraith, the book would almost certainly have continued to languish in obscurity, probably forever.
“So, the basic idea is to randomly throw 9,999 darts at a scale ranging from zero to 500 million and study the resulting distribution of intervals:”
Let me sum the author’s argument. There exists a random manner to divide income that produces an exponential distribution. Therefore, because income is exponentially distributed, it is divided in a random manner. Logical fallacy much?
No, no fallacy. Think of it this way:
When you toss a coin it is physically a very complicated process. You have different acceleration forces, air resistance, friction, mass imbalances in the coin itself and so on and so forth. But in the end the whole process is a very good random experiment because the simplest description is a fifty fifty uniform distribution.
It is the same with wealth: of course you are not throwing darts in real life but it the outcome can very parsimoniously be modelled by throwing darts. It is indistinguishable from throwing darts. So in the same way that the distribution of coin tosses is random the distribution of wealth is random too.
Just a an aside: this way of thinking comes quite naturally to quants (like myself) who model the ups and downs of the stock exchange with probability distributions. Of course the stock exchange too is being driven by all kinds complicated processes (fundamental data, politics, psychology etc.), too complicated to model really. But the result is indistinguishable from luck. This is why chimps throwing darts at stock pages often outperform professional fund managers.
Why 9,999 darts and not 10,000?
Because when you want to divide something into n parts you need n-1 cuts. When you want to divide a chocolate bar into two pieces you need one cut.
Although I agree that showing that a distribution created by pure chance resembles that of wealth distribution does not demonstrate that this is the underlying causal process (note the similarity to the discussion on the neutral theory in ecology, where pure stochasticity can reproduce several patterns), a few studies based on more elaborated models come to the same conclusion (admittedly these just came to my mind when reading the post on r-bloggers and are not based on an exhaustive literature research):
van de Rijt A., Kang S.M., Restivo M. & Patil A. (2014). Field experiments of success-breeds-success dynamics. Proceedings of the National Academy of Sciences 111, 6934–6939. https://doi.org/10.1073/pnas.1316836111
Fargione J. E., Lehman C. & Polasky S. (2011). Entrepreneurs, Chance, and the Deterministic Concentration of Wealth. PloS ONE 6, 1–6
Very interesting, thank you for the references.
I like to think of it this way.
10,000 children are born today, one is my kid, Baby Matt, the other is (say) Baby Trump. In 20 years, Not So Baby Matt is probably working part time and studying, Possibly Still Baby Trump is ‘managing’ a $350m hedge fund. What roll did IQ play in this? Of course that can’t be answered. But one thing we do know, when you take those 10,000 20 year olds and plot their wealth, Possibly Still Baby Trump is all the way over there on the right, irrespective of his/her IQ.
That is certainly a valid way to see it!
On the other hand: Baby Trump will of course be an intelligent baby, in fact it will be the most intelligent baby in the world. There has never been a more intelligent baby in the whole universe. Believe me!